
Bepalingscoëfficiëntformule (inhoudsopgave)
- Formule
- Voorbeelden
Wat is de formule voor de bepaling van de coëfficiënt?
In de statistiek is de determinatiecoëfficiënt, ook wel R2 genoemd, een hulpmiddel dat het vermogen van een statistisch model om toekomstige resultaten te verklaren en te voorspellen bepaalt en beoordeelt. Met andere woorden, als we afhankelijke variabele y en onafhankelijke variabele x in een model hebben, dan helpt R2 bij het bepalen van de variatie in y door variatie x. Het is een van de belangrijkste resultaten van regressieanalyse en wordt gebruikt wanneer we de toekomst willen voorspellen of sommige modellen met gerelateerde informatie willen testen. De waarde van R2 ligt tussen 0 en 1 en hoger dan de waarde van R2, beter zal de voorspelling en sterkte van het model zijn. R2 is zeer vergelijkbaar met de correlatiecoëfficiënt omdat de correlatiecoëfficiënt de directe associatie van twee variabelen meet. R2 is in feite een kwadraat van een correlatiecoëfficiënt.
Formule voor bepaling van de coëfficiënt:
Er zijn meerdere formules om de bepalingscoëfficiënt te berekenen:
- Correlatiecoëfficiënt gebruiken:
Correlation Coefficient = Σ ((X – X m ) * (Y – Y m )) / √ (Σ (X – X m ) 2 * Σ (Y – Y m ) 2 )
Waar:
- X - Gegevenspunten in gegevensset X
- Y - Gegevenspunten in gegevensset Y
- X m - Gemiddelde van gegevensset X
- Y m - Gemiddelde van gegevensset Y
Zo
Coefficient of Determination(R 2 ) = (Correlation Coefficient) 2
- Regressie-uitgangen gebruiken
Bepalingscoëfficiënt (R 2 ) = verklaard variatie / totale variatie
Bepalingscoëfficiënt (R2) = MSS / TSS
Coefficient of Determination (R 2 ) = (TSS – RSS) / TSS
Waar:
- TSS - Total Sum of Squares = Σ (Yi - Ym) 2
- MSS - Model Sum of Squares = Σ (Y - Ym) 2
- RSS - Residual Sum of Squares = Σ (Yi - Y ^) 2
Y is de voorspelde waarde van het model, Yi is de ie-waarde en Ym is de gemiddelde waarde
Voorbeelden van bepalingscoëfficiëntformule (met Excel-sjabloon)
Laten we een voorbeeld nemen om de berekening van de bepalingscoëfficiënt beter te begrijpen.
U kunt deze bepalingscoëfficiënt formule Excel-sjabloon hier downloaden - Bepalingscoëfficiënt formule Excel-sjabloonBepalingscoëfficiëntformule - Voorbeeld # 1
Laten we zeggen dat we twee gegevenssets X & Y hebben en elk 20 willekeurige gegevenspunten bevat. Bereken de bepalingscoëfficiënt voor de gegevensset X & Y.
Gemiddelde wordt berekend als:
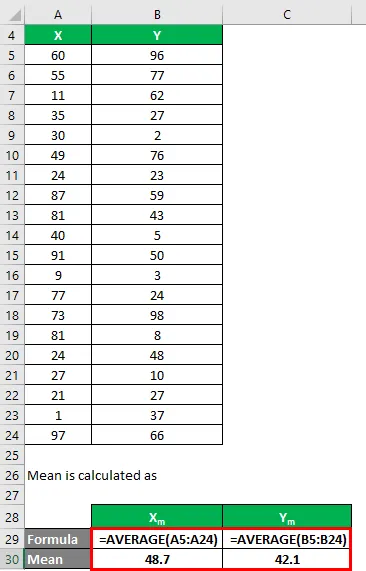
- Gemiddelde van gegevensset X = 48, 7
- Gemiddelde van gegevensset Y = 42, 1
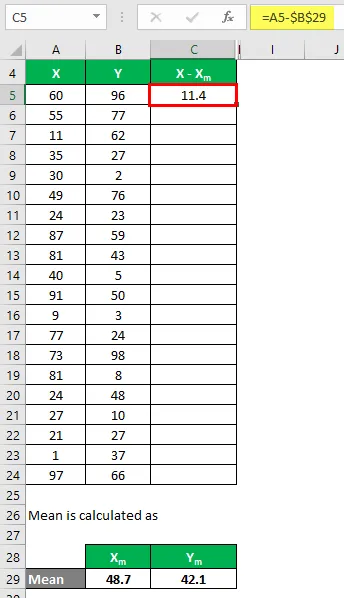
Nu moeten we het verschil tussen de gegevenspunten en de gemiddelde waarde berekenen.
Op dezelfde manier berekenen voor alle gegevensset van X.
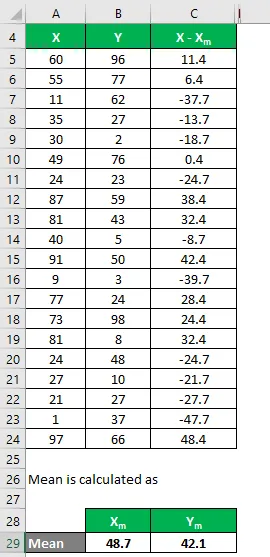
Evenzo, bereken het ook voor dataset Y.

Bereken het kwadraat van het verschil voor zowel de gegevenssets X als Y.
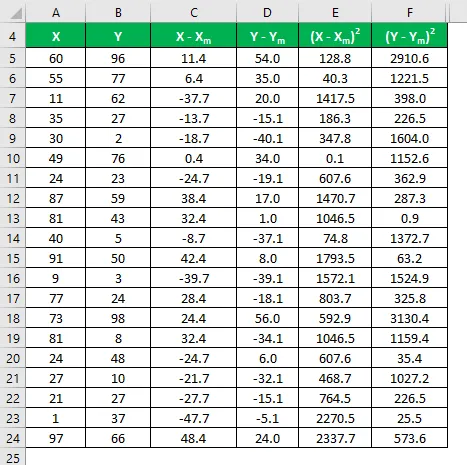
Vermenigvuldig het verschil in X met Y.
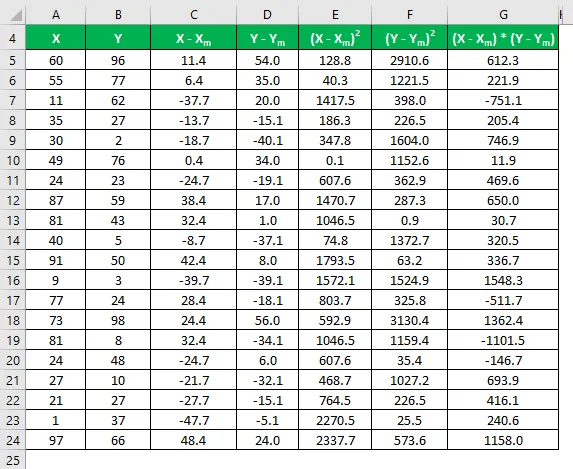
Correlatiecoëfficiënt wordt berekend met behulp van de onderstaande formule
Correlatiecoëfficiënt = Σ ((X - X m ) * (Y - Y m )) / √ (Σ (X - X m ) 2 * Σ (Y - Y m ) 2 )
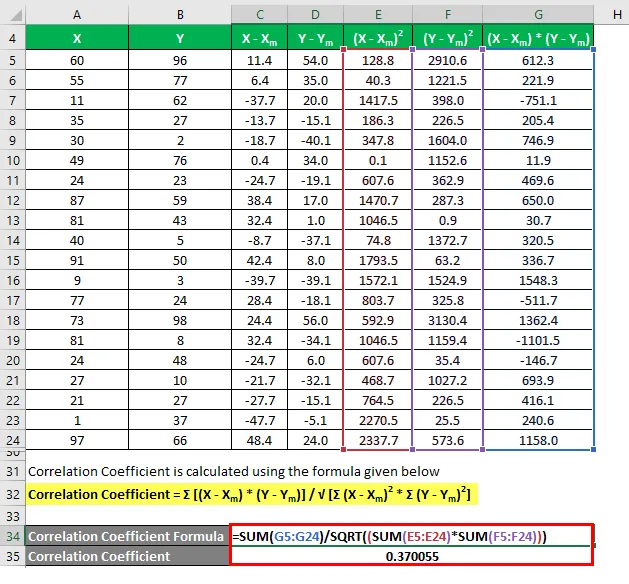
Bepalingscoëfficiënt wordt berekend met behulp van de onderstaande formule
Bepalingscoëfficiënt = (correlatiecoëfficiënt) 2
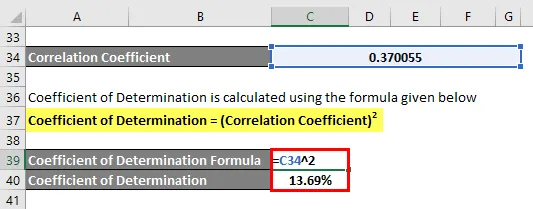
Bepalingscoëfficiënt = 13, 69%
Bepalingscoëfficiëntformule - Voorbeeld # 2
Stel dat u een zeer risicomijdende belegger bent en dat u geld op de aandelenmarkt wilt beleggen. U weet niet zeker in welke aandelen u moet beleggen en ook uw risicobereidheid is laag. U wilt dus beleggen in een aandeel dat veilig is en de prestaties van de index kan nabootsen. Uw vriend, die een actieve belegger is, heeft 3 aandelen voor u genomineerd op basis van zijn fundamentele en technische informatie en u wilt 2 aandelen kiezen uit die drie.
U hebt ook informatie verzameld over hun historische rendementen van de afgelopen 15 jaar.
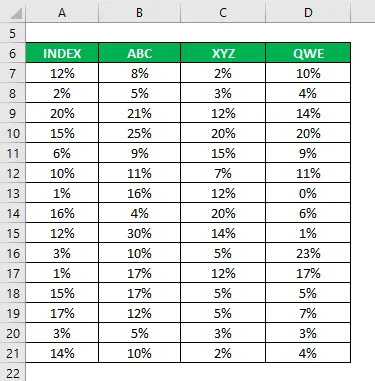
Correlatiecoëfficiënt wordt berekend met behulp van de Excel-formule
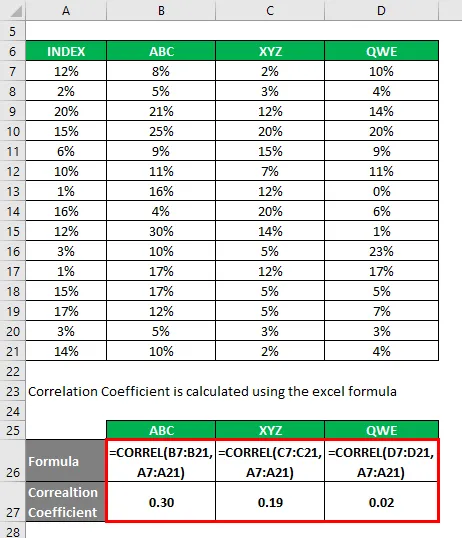
Bepalingscoëfficiënt wordt berekend met behulp van de onderstaande formule
Bepalingscoëfficiënt = (correlatiecoëfficiënt) 2
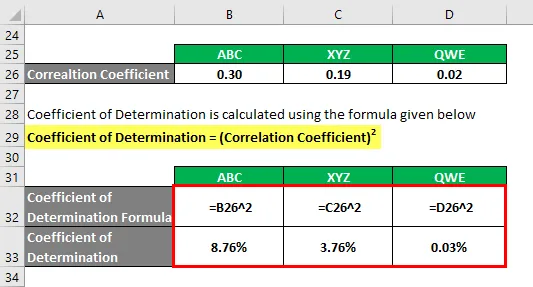
Op basis van de informatie kiest u aandelen ABC en XYZ om te beleggen, omdat deze de hoogste bepalingscoëfficiënt hebben.
Uitleg
Bepalingscoëfficiënt, zoals hierboven uitgelegd, is het kwadraat van de correlatie tussen twee gegevensverzamelingen. Als R2 0 is, betekent dit dat er geen correlatie is en dat onafhankelijke variabele de waarde van de afhankelijke variabele niet kan voorspellen. Evenzo betekent dit dat als de waarde 1 is, onafhankelijke variabele altijd succesvol zal zijn bij het voorspellen van de afhankelijke variabele. Maar er zijn ook enkele beperkingen. Hoewel het ons de correlatie tussen 2 gegevenssets vertelt, vertelt het ons niet of die waarde voldoende is of niet.
Grote waarde R2 betekent ook niet altijd dat de 2 variabelen sterke relaties hebben en dat het een toevalstreffer kan zijn. Bijvoorbeeld: Laten we zeggen dat de R2-waarde tussen een aantal auto's dat in een jaar wordt verkocht en het aantal ijsdozen dat in een jaar wordt verkocht 80% is. Maar er is geen verband tussen deze twee. Je moet dus heel voorzichtig zijn tijdens het gebruik van R2 en eerst de gegevens begrijpen en vervolgens de methode toepassen
Relevantie en gebruik van de formule voor de bepaling van de coëfficiënt
Er zijn veel praktische toepassingen van R2. R2 wordt bijvoorbeeld zeer vaak gebruikt door beleggers om de prestaties van hun portefeuille met de markt te vergelijken en ook toekomstige richtingen te voorspellen. Op dezelfde manier helpt hedgefondsen R2 om hen te helpen het risico in hun modellen te modelleren. Maar uiteindelijk is het resultaat gebaseerd op zuivere cijfers en statistieken die soms misleidend kunnen zijn. Zoals hierboven vermeld, moet eerst worden gecontroleerd of de uitvoer van de R2 in het echte leven zinvol is of niet.
Aanbevolen artikelen
Dit is een leidraad geweest voor de formule van de coëfficiënt van de bepaling. Hier bespreken we hoe de bepalingscoëfficiënt te berekenen, samen met praktische voorbeelden en een downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Gids voor formule voor risicopremie premium
- Voorbeelden van de dekkingsverhoudingformule
- Calculator voor op activiteit gebaseerde kostenformule
- Hoe informatieratio berekenen met behulp van formule?