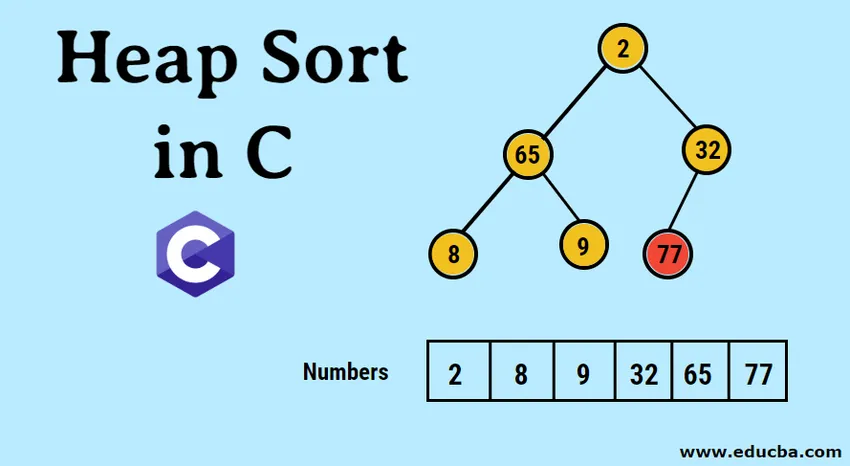
Introductie tot Heap Sort in C
Sorteren is een techniek die draait om het ordenen van elementen op basis van verschillende eigenschappen. (Eigenschappen zoals gegevens ordenen in oplopende, aflopende of alfabetische volgorde). Een belangrijk voorbeeld van sorteren dat we hier kunnen bedenken, is het bestellen van artikelen tijdens online winkelen. We kunnen betrekking hebben op prijzen, populariteit, laatste enzovoort. Er zijn dus veel technieken voor deze positionering van elementen door middel van sorteren. In dit onderwerp gaan we meer te weten komen over Heap Sort in C.
Hier gaan we een van de meest voorkomende sorteertechnieken leren, Heap Sort, via programmeertaal C.
De logica voor Heap Sort
Hoe kunnen we eigenlijk heap-sortering uitvoeren? Laten we hieronder kijken.
Ten eerste is de heap een van de op boom gebaseerde gegevensstructuur. De hier betrokken boom is altijd een complete binaire boom. En er zijn twee soorten hoop
- Min - Heap: algemeen gerangschikt in oplopende volgorde, dat wil zeggen als het bovenliggende knooppuntelement een waarde heeft die lager is dan die van onderliggende knooppuntelementen.
- Max - Heap: algemeen gerangschikt in afnemende volgorde, dat wil zeggen als het bovenliggende knooppuntelement meer waarde heeft dan die van onderliggende knooppuntelementen.
Stappen voor Heap Sort
- Zodra een ongesorteerde lijstgegevens zijn verkregen, worden elementen in de heap-gegevensstructuur georganiseerd, hetzij op basis van het creëren van een min-heap of een max-heap.
- Het eerste element uit de bovenstaande lijst is toegevoegd aan onze array
- Wederom wordt de head-datastructuurtechniek op dezelfde manier gevormd als de eerste stap en opnieuw wordt het hoogste element of het minste element opgepakt en toegevoegd aan onze array.
- Herhaalde stappen helpen ons de array met de gesorteerde lijst te krijgen.
Programma voor heap sorteren in C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Eerst vragen we de gebruiker om het aantal elementen in te voeren dat moet worden gesorteerd, waarna de gebruiker verschillende elementen mag invoeren die moeten worden gesorteerd.
Stappen gevolgd
- De volgende waar we ons op richten is het maken van een heap-array, in dit geval max-heap-array.
- De belangrijkste voorwaarde voor het verkrijgen van een maximale heap-array is om te controleren of geen enkele bovenliggende knooppuntwaarde lager is dan de onderliggende knooppuntwaarde. We gaan ruilen totdat we die voorwaarde hebben bereikt.
- Het belangrijkste voordeel van deze complete binaire structuur is dat de linker en rechter onderliggende knooppunten van een bovenliggend knooppunt toegankelijk zijn met respectievelijk waarden 2 (i) + 1 en 2 * (i) + 2. Waar ik het bovenliggende knooppunt is.
- Dus op deze manier plaatsen we onze wortelknoop met de maximale waarde op de meest rechtse bladknoopplaats. En dan weer dezelfde procedure volgen, zodat het volgende maximale aantal nu het root-knooppunt wordt.
- We gaan dezelfde procedure volgen totdat er nog maar één knooppunt over is in de heap-array.
- En dan rangschikken we onze heap-array om een perfect gesorteerde array in oplopende volgorde te vormen.
- Ten slotte drukken we de gesorteerde array in de uitvoer af.
Output:
De uitgang is hieronder bijgevoegd.
Laat me je de picturale weergave van de gebeurtenissen tonen:
- De ingevoerde gegevens worden eerst als volgt weergegeven in de vorm van een eendimensionale array.

- De afgebeelde weergave van de gevormde binaire boom is als volgt:
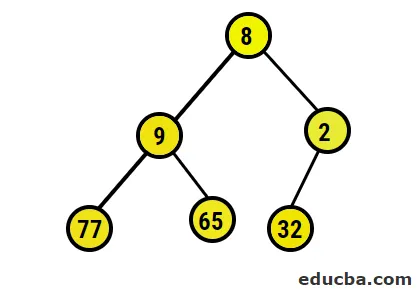
- Nu gaan we converteren naar de maximale heap door ervoor te zorgen dat alle bovenliggende knooppunten altijd groter zijn dan onderliggende knooppunten. Zoals vermeld in de uitvoer onder heap gesorteerde array, zou de grafische weergave zijn:
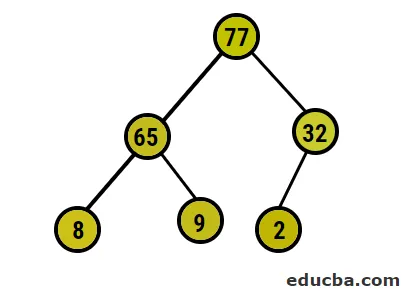
- Hierna gaan we de wortelknoop verwisselen met de extreme bladknoop en deze vervolgens uit de boom verwijderen. De bladknoop zou zo nu en dan de wortel zijn hetzelfde proces e gevolgd om opnieuw het hoogste element in de wortel te krijgen
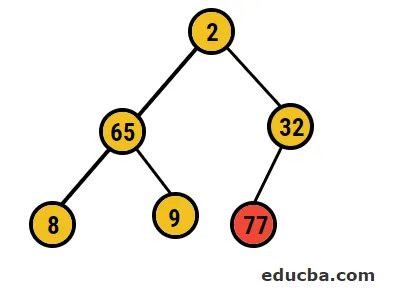
- In dit geval worden dus 77 cijfers uit deze structuur verwijderd en in onze gesorteerde array geplaatst en wordt het proces herhaald.
Het bovenstaande hebben we gezien voor het vormen van max heap array. Hetzelfde proces wordt ook behandeld met de min-heap array formatie. Zoals hierboven besproken, is het enige verschil met de relatie tussen ouder- en kindknooppuntelementen.
Kun je als oefening proberen de heap-soort in de aflopende volgorde te vormen?
Conclusie
Hoewel er veel sorteertechnieken zijn, wordt heap sort beschouwd als een van de betere sorteertechnieken vanwege de complexiteit van tijd en ruimte. De tijdcomplexiteit voor alle beste, gemiddelde en worst case is O (nlogn), waarbij de worst-case complexiteit beter is dan de worst-case complexiteit van Quicksort en de ruimtecomplexiteit O (1) is.
Aanbevolen artikelen
Dit is een gids voor Heap Sort in C. Hier bespreken we de logica en de stappen voor Heap Sort met de voorbeeldcode en uitvoer samen met afbeeldingen. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Heap Sort In Java
- Selectie sorteren op Java
- Palindrome in C-programma
- Patronen in C-programmering
- Heap-sortering in C ++ (algoritme)
- Heap Sort in Python
- C Matrixvermenigvuldiging programmeren