Inleiding tot wiskundige functies in C ++
Het is moeilijk en tijdrovend wanneer u elke keer code moet schrijven om elementaire wiskundige berekeningen in uw programma uit te voeren. Daarom biedt C ++ een groot aantal wiskundige functies om uw code eenvoudig en efficiënt te maken. U kunt een groot aantal bewerkingen op getallen uitvoeren met wiskundige functies. Omdat deze functies zijn ingebouwd en worden ondersteund door de bibliotheek in C ++, is het noodzakelijk om een headerbestand of aan het begin van de code op te nemen om alle functies van wiskundige functies te gebruiken. Het is niet nodig om de logica in code te schrijven om bewerkingen uit te voeren, het is er allemaal in de bibliotheek.
Verschillende soorten wiskundige functies
C ++ biedt een enorm aantal verschillende soorten wiskundige functies die hieronder worden genoemd met voorbeelden:
1. Maximale en minimale functie
- max (p, q): het retourneert een maximumaantal tussen p en q.
- min (p, q): het retourneert een minimumaantal tussen p en q.
C ++ Code om bovenstaande functionaliteit te implementeren
#include
#include
using namespace std;
int main() (
cout << max(16, 18) << "\n";
cout << min(16, 18) << "\n";
return 0;
)
Output:

2. Stroomfuncties
- pow (m, n): het berekent m verhoogd tot de macht n.
- sqrt (m): het berekent de vierkantswortel van m.
- cbrt (n): het berekent de kubuswortel van n.
- hypot (m, n): het berekent de hypotenusa van de rechthoekige driehoek.
C ++ code om bovenstaande functionaliteit te implementeren
#include
#include
using namespace std;
int main() (
cout << pow(2, 3) << "\n";
cout << sqrt(16) << "\n";
cout << cbrt(27) << "\n";
cout << hypot(3, 4) << "\n";
return 0;
)
Output:

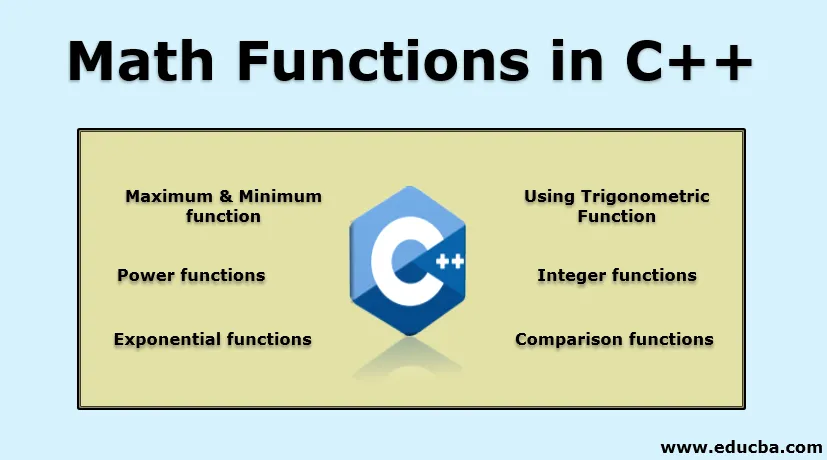
3. Exponentiële functies
- exp (p): het berekent de exponentiële e verhoogd naar macht p.
- log (p): het berekent de logaritme van p.
- log10 (p): het berekent de gemeenschappelijke logaritme van p.
- exp2 (p): het berekent de exponentiële basis 2 van p.
- log2 (p): het berekent de logaritme van basis 2 van p.
- logb (p): het berekent de logaritme van p.
C ++ code om bovenstaande functionaliteit te implementeren
#include
#include
using namespace std;
int main() (
cout << exp(5) << "\n";
cout << log(8) << "\n";
cout << log10(8) << "\n";
cout << exp2(5) << "\n";
cout << log2(8) << "\n";
cout << logb(8) << "\n";
return 0;
)
Output:
4. Geheel getalfuncties
Het helpt bij het vinden van de dichtstbijzijnde gehele waarde.
- eiling (z): hiermee wordt de waarde van z afgerond.
- verdieping (z): het rondt de waarde van z naar beneden af.
- round (z): rondt de waarde van z af.
- fmod (z, y): het berekent de rest van deling z / y.
- trunc (z): het zal de z-waarde naar nul afronden.
- rint (z): hiermee wordt de z-waarde afgerond met de afrondingsmodus.
- nearbyint (z): hiermee wordt de z-waarde afgerond naar een nabije integraalwaarde.
- rest (z, y): het berekent de rest van z / y.
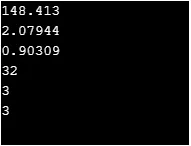
C ++ code om bovenstaande functionaliteit te implementeren
#include
#include
using namespace std;
int main() (
cout << ceil(4580.01) << "\n";
cout << floor(151.999) << "\n";
cout << round(518.5) << "\n";
cout << fmod(5, 21) << "\n";
cout << trunc(20.25) << "\n";
cout << rint(21.25) << "\n";
cout << nearbyint(182.55) << "\n";
cout << remainder(12, 36) << "\n";
return 0;
)
Output:
5. Vergelijkingsfuncties
Hulp bij het snel vergelijken van getallen maakt niet uit hoe lang het nummer is. Hieronder volgen enkele voorbeelden van vergelijkingsfuncties:
- isgreater (p, q): het controleert of p groter is dan q of niet.
- islessequal (p, q): hiermee wordt gecontroleerd of p kleiner is dan of gelijk is aan q of niet.
- isgreaterequal (p, q): het controleert of p groter is dan of gelijk is aan q of niet.
- islessgreater (p, q): het controleert of p kleiner of groter is dan y of niet.
- isonordered (p, q): het controleert of p wordt vergeleken of niet.
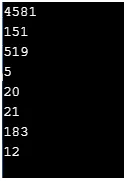
C ++ code om bovenstaande functionaliteit te implementeren
#include
#include
using namespace std;
int main() (
// cout << less(22, 29) << "\n";
cout << isgreater(48, 47)<< "\n";
cout << islessequal(11, 5)<< "\n";
cout << isgreaterequal(19, 72)<< "\n";
cout << islessgreater(59, 84)<< "\n";
cout << isunordered(62, 84)<< "\n";
return 0;
)
Output:

6. Gebruik van trigonometrische functie
Functies speciaal gebruikt in geometrische berekeningen. De rechthoekige driehoek geeft een relatie tussen hoek en de verhouding van de lengte van de twee zijden.
- sin (y): het zal de waarde van sinus y berekenen.
- cos (y): het berekent de waarde van cosinus y.
- tan (y): het berekent de waarde van raaklijn y.
- asin (y): het berekent de waarde van inverse sinus y.
- acos (y): het berekent de waarde van inverse cosinus y.
- atan (y): het berekent de waarde van inverse tangens y.
- atan2 (y, x): het berekent de waarde van de inverse tangens van y- en x-coördinaten.
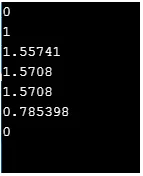
C ++ code om bovenstaande functionaliteit te implementeren
#include
#include
using namespace std;
int main() (
cout << sin(0) << "\n";
cout << cos(0) << "\n";
cout << tan(1) << "\n";
cout << asin(1)<< "\n";
cout << acos(0)<< "\n";
cout << atan(1)<< "\n";
cout << atan2(0, 1)<< "\n";
return 0;
)
Output:
Hier zijn enkele interessantere functies die helpen bij het berekenen van waarden van hyperbolische trigonometrische functies en ze worden hyperbolische functies genoemd.
- sinh (x): het zal de waarde van de hyperbolische sinus van x berekenen.
- cosh (x): het berekent de waarde van de hyperbolische cosinus van x.
- tanh (x): het berekent de waarde van de hyperbolische tangens van x.
- asinh (x): het berekent de waarde van de hyperbolische boogsinus van x.
- acosh (x): het berekent de waarde van de cosinus hyperbolische boog van x.
- atanh (x): het berekent de waarde van de hyperbolische boogsinus van x.
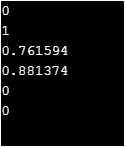
C ++ code om bovenstaande functionaliteit te implementeren
#include
#include
using namespace std;
int main() (
cout << sinh(0)<< "\n";
cout << cosh(0)<< "\n";
cout << tanh(1)<< "\n";
cout << asinh(1)<< "\n";
cout << acosh(1)<< "\n";
cout << atanh(0)<< "\n";
return 0;
)
Output:
Conclusie
Wiskundige functies spelen een belangrijke rol bij het opslaan van een enorme hoeveelheid tijd en ruimte in het geheugen. Alle functies zijn ingebouwd, het is niet nodig om direct een wiskundige functie te gebruiken, gewoon door een header-bestand toe te voegen dat de optie geeft om de hele bibliotheek van wiskundeklasse te gebruiken.
Aanbevolen artikelen
Dit is een handleiding voor wiskundige functies in C ++. Hier bespreken we dat de C ++ een groot aantal verschillende soorten wiskundige functies met voorbeelden biedt. U kunt ook onze andere voorgestelde artikelen doornemen -
- Overschrijven in C ++
- Overbelasting in C ++
- Vierkantswortel in C ++
- Arrays in C ++
- Overbelasting in Java
- Vierkantswortel in PHP
- Top 11 kenmerken en voordelen van C ++
- Gids voor vierkantswortel in JavaScript