
Inleiding tot grafiek in gegevensstructuur
Grafieken zijn niet-lineaire gegevensstructuren die een eindige set knopen en randen bevatten. De knopen zijn de elementen en randen zijn geordende paren verbindingen tussen de knopen.
Let op het woord niet-lineair. Een niet-lineaire gegevensstructuur is een structuur waarbij de elementen niet in opeenvolgende volgorde zijn gerangschikt. Een array is bijvoorbeeld een lineaire gegevensstructuur omdat de elementen achter elkaar zijn gerangschikt. U kunt in één run alle elementen van een array doorlopen. Dat is niet het geval bij niet-lineaire gegevensstructuren. De elementen van een niet-lineaire gegevensstructuur zijn gerangschikt op meerdere niveaus, vaak volgens een hiërarchisch patroon. Grafieken zijn niet-lineair.
Het volgende woord om op te letten is eindig. We definiëren de grafiek om een eindig en telbaar aantal knooppunten te hebben. Dit is een nogal onaangename term. In wezen kan een grafiek een oneindig aantal knooppunten hebben en toch eindig zijn. Bijvoorbeeld een stamboom die teruggaat tot Adam en Eva. Dit is een relatief oneindige grafiek, maar kan nog steeds worden geteld en wordt daarom als eindig beschouwd.
Voorbeeld uit de echte wereld
Het beste voorbeeld van grafieken in de echte wereld is Facebook. Elke persoon op Facebook is een knooppunt en is verbonden via randen. A is een vriend van B. B is een vriend van C enzovoort.
terminologieën
Hier zijn de onderstaande terminologie van grafiek in de datastructuur
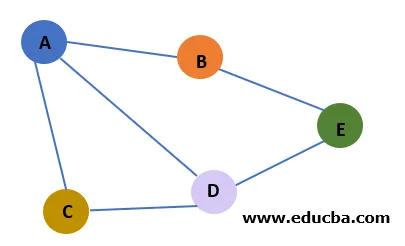
1. Grafische weergave : in het algemeen wordt een grafiek weergegeven als een paar sets (V, E). V is de reeks hoekpunten of knopen. E is de verzameling randen. In het bovenstaande voorbeeld
V = (A, B, C, D, E)
E = (AB, AC, AD, BE, CD, DE)
2. Knooppunt of hoekpunt: de elementen van een grafiek zijn verbonden door randen.
3. Randen: een pad of een lijn tussen twee hoekpunten in een grafiek.
4. Aangrenzende knooppunten: twee knooppunten worden aangrenzend genoemd als ze via een rand zijn verbonden. In het bovenstaande voorbeeld grenst knooppunt A aan knooppunten B, C en D, maar niet aan knooppunt E.
5. Pad: pad is een reeks randen tussen twee knooppunten. Het is in wezen een doorgang die begint bij de ene knoop en eindigt bij de andere. In het bovenstaande voorbeeld zijn er meerdere paden van knooppunt A naar knooppunt E.
Pad (A, E) = (AB, BE)
OF
Pad (A, E) = (AC, CD, DE)
OF
Pad (A, E) = (AD, DE)
6. Niet-gerichte grafiek: een niet-gerichte grafiek is een grafiek waarbij de randen geen specifieke richting aangeven. De randen zijn bidirectioneel.
Voorbeeld
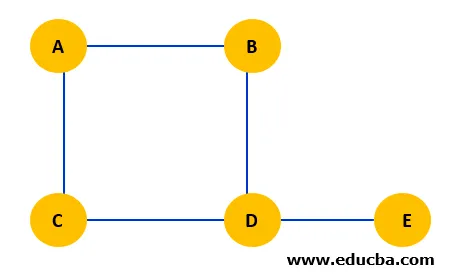
In dit voorbeeld kan de rand AC dus zowel van A naar C als van C naar A worden verplaatst. Vergelijkbaar met alle randen. Een pad van knooppunt B naar knooppunt C is (BA, AC) of (BD, DC).
7. Gerichte grafiek: een gerichte grafiek is een grafiek waarbij de randen alleen in een opgegeven richting kunnen worden verplaatst.
Voorbeeld
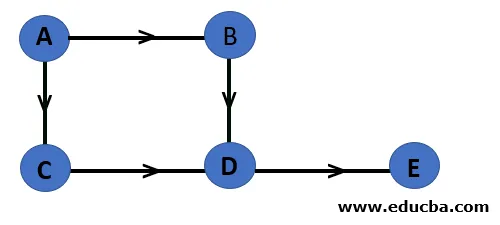
Dus in hetzelfde voorbeeld zijn de randen nu directioneel. U kunt de rand alleen in de richting ervan verplaatsen. Er is nu geen pad van knooppunt B naar knooppunt C.
8. Gewogen grafiek: een gewogen grafiek is een grafiek waarbij de randen zijn gekoppeld aan een gewicht. Dit zijn meestal de kosten om de rand te doorkruisen.
Voorbeeld
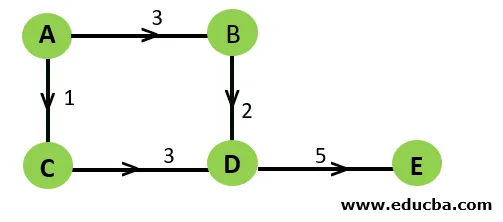
In hetzelfde voorbeeld hebben de randen nu dus een bepaald gewicht. Er zijn twee mogelijke paden tussen knooppunt A naar knooppunt E.
Pad1 = (AB, BD, DE), Gewicht1 = 3 + 2 + 5 = 10
Pad2 = (AC, CD, DE), Gewicht2 = 1 + 3 + 5 = 9
Het is duidelijk dat men de voorkeur geeft aan Path2 als het doel is om knooppunt E te bereiken vanaf knooppunt A met minimale kosten.
Basishandelingen op grafiek
Hier zijn de onderstaande basisbewerkingen van de grafiek
1. Toevoegen / verwijderen Vertex
Dit is de eenvoudigste bewerking in de grafiek. U voegt eenvoudig een hoekpunt toe aan een grafiek. Het hoeft niet via een rand met een ander hoekpunt te zijn verbonden. Wanneer u een hoekpunt verwijdert, moet u alle randen verwijderen die afkomstig zijn van en eindigen op het verwijderde hoekpunt.
2. Rand toevoegen / verwijderen
Met deze bewerking wordt een rand tussen twee hoekpunten toegevoegd of verwijderd. Wanneer alle randen die afkomstig zijn van en eindigen op een hoekpunt worden verwijderd, wordt het hoekpunt een geïsoleerd hoekpunt.
3. Breedte-eerste zoekopdracht (BFS)
Dit is een transversale bewerking in de grafiek. BFS loopt horizontaal door de grafiek. Dit betekent dat het alle knooppunten op één niveau doorloopt voordat het naar het volgende niveau gaat.
Het BFS-algoritme begint bovenaan de eerste knoop in de grafiek en doorloopt vervolgens alle aangrenzende knooppunten. Nadat alle aangrenzende knooppunten zijn doorlopen, herhaalt het algoritme dezelfde procedure voor onderliggende knooppunten.
Voorbeeld
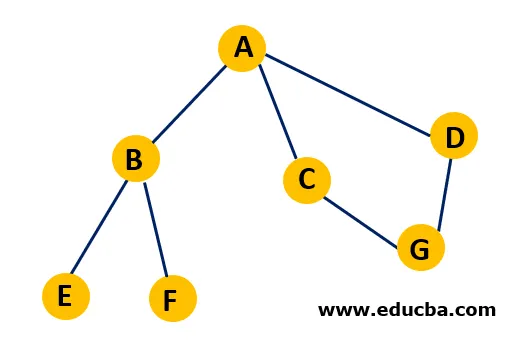
Het doorlopen van de bovenstaande grafiek op BFS-manier zou resulteren uit A -> B -> C -> D -> E -> F -> G. Het algoritme begint bij knooppunt A en doorloopt alle aangrenzende knooppunten B, C en D. Het markeert alle vier knooppunten zoals bezocht. Zodra alle aangrenzende knooppunten van A zijn doorlopen, verplaatst het algoritme zich naar het eerste aangrenzende knooppunt van A en herhaalt dezelfde procedure. In dit geval is het knooppunt B en zijn de aangrenzende knooppunten naar B E en F. Vervolgens worden de aangrenzende knooppunten naar C doorkruist. Zodra alle knooppunten zijn bezocht, eindigt de bewerking.
4. Depth First Search (DFS)
Depth First Search of DFS doorloopt de grafiek verticaal. Het begint met het hoofdknooppunt of het eerste knooppunt van de grafiek en doorloopt alle onderliggende knooppunten voordat het naar de aangrenzende knooppunten wordt verplaatst.
Voorbeeld
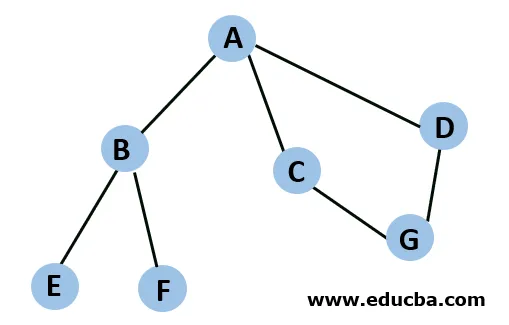
Het doorlopen van de bovenstaande grafiek op BFS-manier zou resulteren uit A -> B -> E -> F -> C -> G -> D. Het algoritme begint vanaf knooppunt A en doorloopt alle onderliggende knooppunten. Zodra het B tegenkomt, lijkt het dat het verdere kindknooppunten heeft. De kindknooppunten van B worden dus doorlopen voordat ze doorgaan naar het volgende kindknooppunt van A.
Real-World implementaties van grafieken
- Ontwerp van elektrische circuits voor krachtoverbrenging.
- Ontwerp van een netwerk van onderling verbonden computers.
- Studie van de moleculaire, chemische en cellulaire structuur van elke stof, bijvoorbeeld menselijk DNA.
- Ontwerp van transportroutes tussen steden en plaatsen binnen een stad.
Conclusie - Grafiek in gegevensstructuur
Grafieken zijn een zeer nuttig concept in gegevensstructuren. Het heeft praktische implementaties op bijna elk gebied. Het is erg belangrijk om de basisprincipes van de grafentheorie te begrijpen, om inzicht te krijgen in de algoritmen van de grafische structuur.
Dit artikel was slechts een inleiding tot grafieken. Het is maar een opstapje. Het wordt aanbevolen om verder te duiken in het onderwerp grafische theorie.
Aanbevolen artikelen
Dit is een gids voor de grafiek in gegevensstructuur. Hier bespreken we de terminologieën en basisbewerkingen van Graph in Data Structure. U kunt ook het volgende artikel bekijken voor meer informatie -
- Sollicitatievragen voor Data Structure
- Gegevensmodel in Cassandra
- Wat is Data Mart?
- Wat is een datawetenschapper?