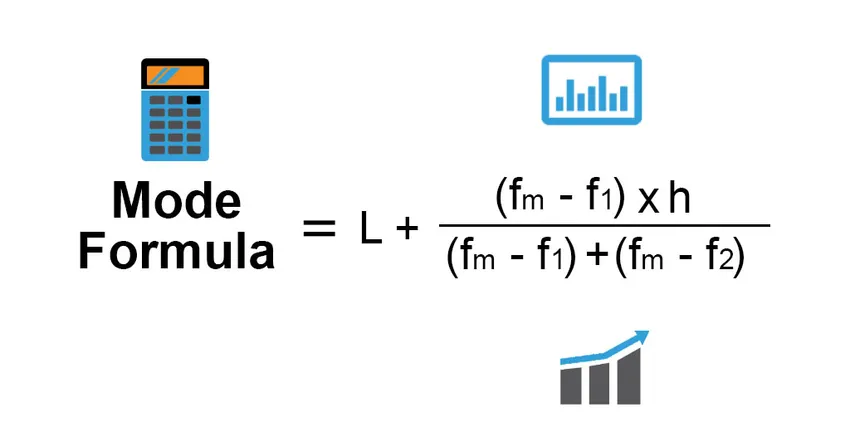
Modusformule (inhoudsopgave)
- Formule
- Voorbeelden
- Rekenmachine
Wat is de modusformule?
De drie centrale maten van neiging zijn gemiddelde mediaan en modus. Wanneer alle drie samen worden gebruikt om een zinvolle analyse in de gegevensset te extraheren. Vandaag zullen we in dit artikel de modus bespreken, die ook een van de sleutels is en de belangrijke centrale tendens die wordt gebruikt. Modus verwijst naar de meest voorkomende waarde in de gegevensset. Modus van een gegevens kan worden gevonden met normale gegevensset, groepgegevensset en niet-gegroepeerde of niet-gegroepeerde gegevensset. Het gemiddelde dat het meest wordt gebruikt, blijft echter de beste maat voor centrale neiging ondanks het bestaan van gemiddelde, mediaan en modus. In dit artikel proberen we de modusfunctie, voorbeelden en uitleg van elk voorbeeld te begrijpen, samen met de formule en de berekeningen.
De formule voor modus is: -
Mode = L + (fm−f1)h /(fm−f1)+(fm−f2)
Modusformule voor gegroepeerde gegevens:
Modus = L + (fm − f1) h / 2fm − f1 − f2
Waar,
- L = Ondergrensmodus van modale klasse
- fm = frequentie van modale klasse
- f1 = Frequentie van klasse voorafgaand aan de modale klasse
- f2 = Frequentie van klasse die de modale klasse opvolgt
- h = Grootte van klasse-interval
Voorbeelden van modusformule (met Excel-sjabloon)
Laten we een voorbeeld nemen om de berekening van de modus op een betere manier te begrijpen.
U kunt deze modusformule Excel-sjabloon hier downloaden - modusformule Excel-sjabloonModusformule - Voorbeeld # 1
Waar de modus wordt berekend, is eenvoudig het aantal waarnemingen in een gegevensset dat meestal voorkomt.
Bereken de modus van de volgende gegevensset.
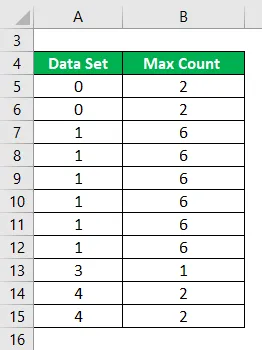
Oplossing:
Een modus wordt berekend als:
Aantal waarnemingen in een gegevensset die meestal voorkomt
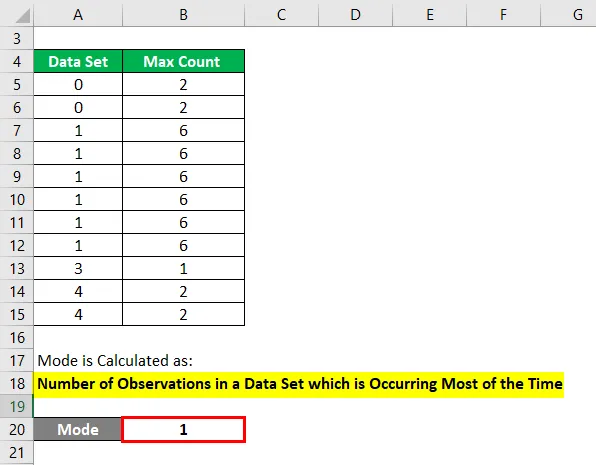
- Modus = 1
Modusformule - Voorbeeld # 2
Bereken de modus met behulp van de gegeven informatie.
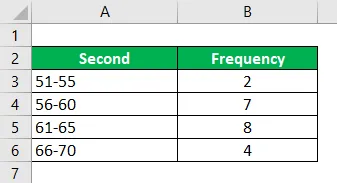
Oplossing:
Opmerking: - Eerst moet de modale groep met de hoogste frequentie worden geïdentificeerd. Als het interval niet continu is, moet 0, 5 worden afgetrokken van de onderste limietmodus en 0, 5 moet worden toegevoegd van de bovenste limietmodus. Dan zal het interval zijn
Modal Group wordt berekend als:
Modale groep die het meest voorkomt, dwz 60.5-65.5
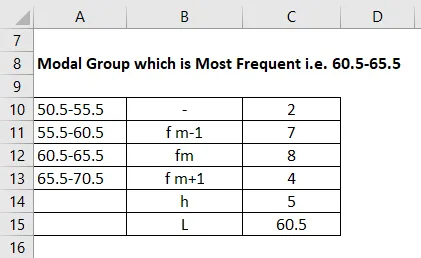
Dan is de lagere frequentie van de modale groep die 4 is, in dit geval wordt fm + 1 genomen en zal fm-1 in dit voorbeeld 7 worden. En we hebben fm, dat is de frequentie 8. De (h) wordt de grootte van het klasse-interval genoemd 5 en we hebben ook rekening gehouden met het startinterval. L is 60, 5.
De modus wordt berekend met behulp van de onderstaande formule
Modus = L + (fm − f1) h / (fm − f1) + (fm − f2)
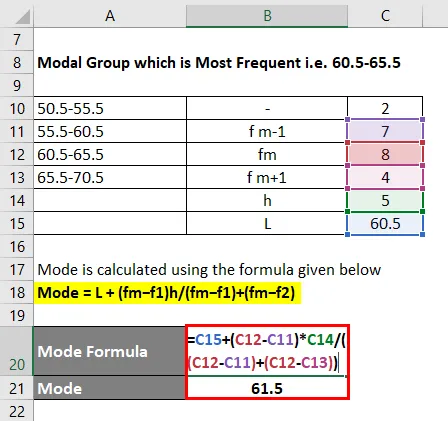
- Modus = 60.5 + (8 - 7) * 5 / ((8 - 7) + (8 - 4))
- Modus = 61, 5
Modusformule - Voorbeeld # 3
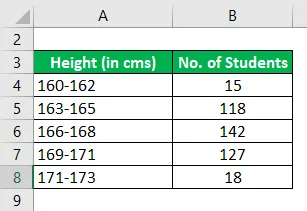
De volgende zijn de hoogteverdelingen in een bepaalde klasse studenten in een bepaalde modus
Bereken de modus met behulp van de gegeven informatie.
Oplossing:
Als het interval niet continu is, moet 0, 5 van de onderste limietmodus worden afgetrokken en 0, 5 moet van de bovenste limietmodus worden opgeteld. Dan zal het interval zijn
Modal Group wordt berekend als:
Modale groep die het meest voorkomt, dwz 165.5-168.5
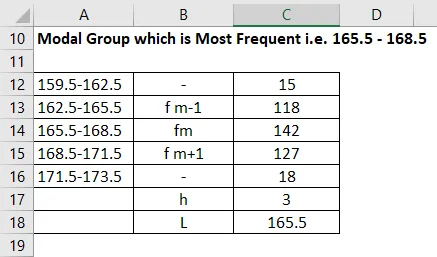
De modus wordt berekend met behulp van de onderstaande formule
Modus = L + (fm − f1) h / (fm − f1) + (fm − f2)
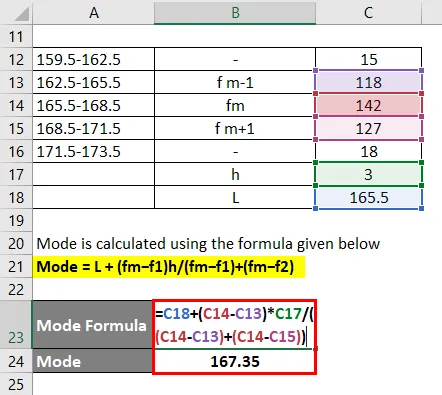
- Modus = 165.5 + (142 - 118) * 3 / (142 - 118) + (142 - 127)
- Modus = 167, 35
Uitleg
De modus kan eenvoudig worden verklaard als de waarde die het meest voorkomt in de gegevensset. En de modus hierboven kan worden verklaard, want als gegevens een groep zijn, moeten we eerst de modale functie berekenen en ook de gegevens continu maken om de modus van de gegevens te berekenen. De modale klasse wordt bepaald met de klasse die de hoogste frequentie in de gegevensset heeft.
Relevantie en gebruik van de modusformule
- Gemiddelde, mediaan en modus onthullen verschillende aspecten van uw gegevens. Iedereen zal je een algemeen idee geven, maar kan je misleiden; met alle drie krijg je een completer beeld
- Voor een normale verdeling hebben de modus, gemiddelde, mediaan dezelfde waarde, omdat Modus een normale verdeling is. De analysemodus op zichzelf weerspiegelt niet het ware beeld. Als u de volledige gegevensset wilt analyseren, moeten alle drie statistische metingen in detail worden geanalyseerd en geïnterpreteerd
- De modus is gemakkelijk te begrijpen en eenvoudig te berekenen.
- De modus wordt niet beïnvloed door extreem grote of kleine waarden.
- De modus kan alleen worden gevonden door inspectie in niet-gegroepeerde gegevens en discrete frequentieverdeling.
- De modus kan nuttig zijn voor kwalitatieve gegevens.
- De modus kan worden berekend in een open-end frequentietabel.
- De modus kan grafisch worden geplaatst
- Mode wordt het meest gebruikt door datawetenschappers
- Modus is dat het ons geen zeer goede maat van centrale neiging zal geven wanneer het meest voorkomende merkteken ver weg is van de rest van de gegevens in de gegevensverzameling
Modus Formule Calculator
U kunt de volgende modusformulecalculator gebruiken
| L | |
| fm | |
| f1 | |
| f2 | |
| h | |
| Modus Formule | |
| Modusformule = | L + (fm - f1) xh / (fm - f1) + (fm - f2) |
| = | 0 + (0 - 0) x 0 / (0 - 0) + (0 - 0) = 0 |
Aanbevolen artikelen
Dit is een gids voor Mode Formula. Hier bespreken we hoe u de modusformule kunt berekenen, samen met praktische voorbeelden. We bieden ook een moduscalculator met een downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Voorbeelden van de Gordon Growth Model Formula
- Formule om het prijsmodel voor kapitaalactiva te berekenen
- Calculator voor totale kostenratioformule
- Poisson-distributieformule (voorbeelden met Excel-sjabloon)