Verschil tussen lineaire regressie versus logistieke regressie
Het volgende artikel Lineaire regressie versus logistieke regressie biedt de belangrijkste verschillen tussen beide, maar voordat we zullen zien wat betekent regressie?
regressie
Regressie is in feite een statistische maat om de sterkte te bepalen van de relatie tussen een afhankelijke variabele, dat wil zeggen de output Y en een reeks andere onafhankelijke variabelen, bijvoorbeeld X 1, X 2 enzovoort. Regressie-analyse wordt in principe gebruikt voor voorspelling en voorspelling.
Wat is lineaire regressie?
Lineaire regressie is een algoritme dat is gebaseerd op het begeleide leerdomein van machine learning. Het neemt een lineair verband over tussen zijn invoervariabelen en de enkele uitvoervariabele waarbij de uitvoervariabele van nature continu is. Het wordt gebruikt om de waarde van de uitgang te voorspellen, laten we zeggen Y uit de ingangen, laten we zeggen X. Wanneer slechts een enkele ingang wordt beschouwd, wordt dit eenvoudige lineaire regressie genoemd.
Het kan worden ingedeeld in twee hoofdcategorieën:
1. Eenvoudige regressie
Werkingsprincipe: Het belangrijkste doel is om de vergelijking te vinden van een rechte lijn die het beste bij de steekproefgegevens past. Deze vergelijking beschrijft algebraïsch de relatie tussen de twee variabelen. De best passende rechte lijn wordt regressielijn genoemd.
Y = β 0 + β 1 X
Waar,
β vertegenwoordigt de functies
P 0 vertegenwoordigt het onderscheppen
β 1 vertegenwoordigt de coëfficiënt van kenmerk X
2. Multivariabele regressie
Het wordt gebruikt om een verband te voorspellen tussen meer dan één onafhankelijke variabele en één afhankelijke variabele. Regressie met meer dan twee onafhankelijke variabelen is gebaseerd op de vorm die past bij de constellatie van gegevens op een multidimensionale grafiek. De vorm van regressie moet zodanig zijn dat deze de afstand van de vorm vanaf elk gegevenspunt minimaliseert.
Een lineair relatiemodel kan wiskundig worden weergegeven zoals hieronder:
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ……. + β n X n
Waar,
β vertegenwoordigt de functies
P 0 vertegenwoordigt het onderscheppen
β 1 vertegenwoordigt de coëfficiënt van kenmerk X1
β n vertegenwoordigt de coëfficiënt van kenmerk Xn
Voor- en nadelen van lineaire regressie
Hieronder worden voordelen en nadelen gegeven:
voordelen
- Vanwege zijn eenvoud wordt het veel gebruikt voor het voorspellen en afleiden van modellen.
- Het richt zich op data-analyse en data preprocessing. Het gaat dus om verschillende gegevens zonder zich druk te maken over de details van het model.
nadelen
- Het werkt efficiënt wanneer de gegevens normaal worden verspreid. Voor efficiënte modellering moet dus de collineariteit worden vermeden.
Wat is logistieke regressie?
Het is een vorm van regressie waarmee afzonderlijke variabelen kunnen worden voorspeld door een combinatie van continue en discrete voorspellers. Het resulteert in een unieke transformatie van afhankelijke variabelen die niet alleen het schattingsproces beïnvloedt, maar ook de coëfficiënten van onafhankelijke variabelen. Het behandelt dezelfde vraag die meervoudige regressie doet, maar zonder verdelingsaannames over de voorspellers. Bij logistieke regressie is de uitkomstvariabele binair. Het doel van de analyse is om de effecten van meerdere verklarende variabelen te beoordelen, die numeriek of categorisch of beide kunnen zijn.
Soorten logistieke regressie
Hieronder staan de 2 soorten logistieke regressie:
1. Binaire logistieke regressie
Het wordt gebruikt wanneer de afhankelijke variabele dichotoom is, dwz als een boom met twee takken. Het wordt gebruikt wanneer de afhankelijke variabele niet-parametrisch is.
Wanneer gebruikt
- Als er geen lineariteit is
- Er zijn slechts twee niveaus van de afhankelijke variabele.
- Als multivariate normaliteit twijfelachtig is.
2. Multinomiale logistieke regressie
Multinomiale logistische regressieanalyse vereist dat de onafhankelijke variabelen metrisch of dichotoom zijn. Het maakt geen veronderstellingen over lineariteit, normaliteit en homogeniteit van variantie voor de onafhankelijke variabelen.
Het wordt gebruikt wanneer de afhankelijke variabele meer dan twee categorieën heeft. Het wordt gebruikt om relaties tussen een niet-metrische afhankelijke variabele en metrische of dichotome onafhankelijke variabelen te analyseren en vergelijkt vervolgens meerdere groepen door een combinatie van binaire logistische regressies. Uiteindelijk biedt het een set coëfficiënten voor elk van de twee vergelijkingen. De coëfficiënten voor de referentiegroep zijn alle nullen. Ten slotte wordt voorspelling gedaan op basis van de hoogste resulterende waarschijnlijkheid.
Voordeel van logistieke regressie: het is een zeer efficiënte en veel gebruikte techniek omdat het niet veel rekenbronnen vereist en geen afstemming vereist.
Nadeel van logistieke regressie: het kan niet worden gebruikt voor het oplossen van niet-lineaire problemen.
Head-to-Head vergelijking tussen lineaire regressie versus logistieke regressie (infographics)
Hieronder staan de top 6 verschillen tussen lineaire regressie versus logistieke regressie 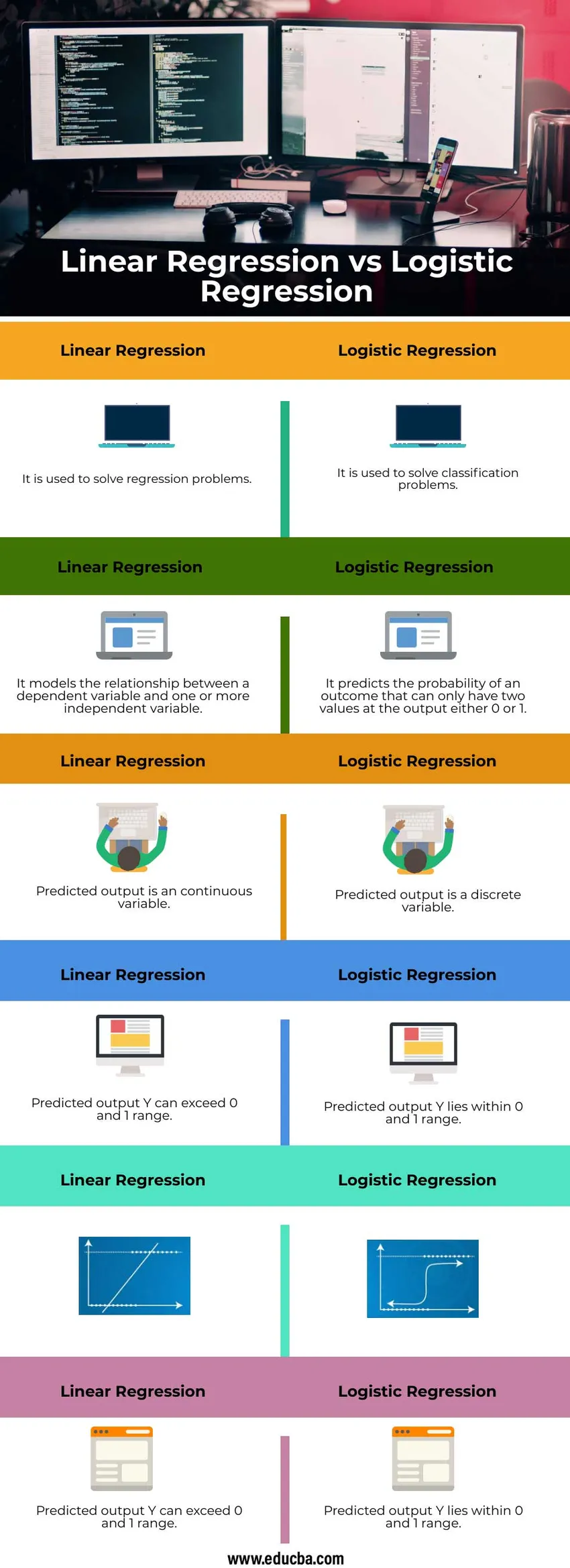
Belangrijk verschil tussen de lineaire regressie versus logistieke regressie
Laten we enkele van de belangrijkste belangrijkste verschillen tussen lineaire regressie versus logistieke regressie bespreken
Lineaire regressie
- Het is een lineaire benadering
- Het gebruikt een rechte lijn
- Er zijn geen categorische variabelen nodig
- Het moet waarnemingen met ontbrekende waarden van de numerieke onafhankelijke variabele negeren
- Uitgang Y wordt gegeven als
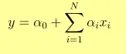
- 1 eenheid toename in x verhoogt Y met α
toepassingen
- De prijs van een product voorspellen
- Score voorspellen in een wedstrijd
Logistieke regressie
- Het is een statistische benadering
- Het gebruikt een sigmoïde functie
- Het kan categorische variabelen bevatten
- Het kan beslissingen nemen, zelfs als er waarnemingen met ontbrekende waarden aanwezig zijn
- Uitgang Y wordt gegeven als, waar z wordt gegeven als
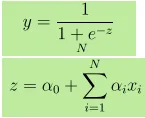
- 1 eenheid toename in x verhoogt Y met logkansen van α
- Als P de waarschijnlijkheid van een gebeurtenis is, dan is (1-P) de waarschijnlijkheid dat deze niet optreedt. Kans op succes = P / 1-P
toepassingen
- Voorspellen of het vandaag zal regenen of niet.
- Voorspellen of een e-mail spam is of niet.
Lineaire regressie versus logistieke regressievergelijkingstabel
Laten we de topvergelijking tussen lineaire regressie versus logistieke regressie bespreken
|
Lineaire regressie |
Logistieke regressie |
| Het wordt gebruikt om regressieproblemen op te lossen | Het wordt gebruikt om classificatieproblemen op te lossen |
| Het modelleert de relatie tussen een afhankelijke variabele en een of meer onafhankelijke variabelen | Het voorspelt de kans op een uitkomst die slechts twee waarden aan de uitgang kan hebben, 0 of 1 |
| De voorspelde uitvoer is een continue variabele | De voorspelde uitvoer is een discrete variabele |
| Voorspelde uitgang Y kan 0 en 1 bereik overschrijden | Voorspelde uitgang Y ligt binnen het bereik van 0 en 1 |
 | 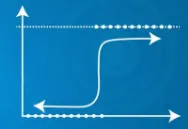 |
| Voorspelde uitgang Y kan 0 en 1 bereik overschrijden | Voorspelde output |
Conclusie
Als functies niet bijdragen aan voorspelling of als ze sterk met elkaar zijn gecorreleerd, voegt dit ruis aan het model toe. Functies die niet genoeg bijdragen aan het model moeten dus worden verwijderd. Als onafhankelijke variabelen sterk gecorreleerd zijn, kan dit een probleem van multi-collineariteit veroorzaken, wat kan worden opgelost door afzonderlijke modellen met elke onafhankelijke variabele te gebruiken.
Aanbevolen artikelen
Dit is een leidraad geweest voor lineaire regressie versus logistieke regressie. Hier bespreken we de belangrijkste verschillen tussen lineaire regressie en logistieke regressie met infographics en vergelijkingstabel. U kunt ook de volgende artikelen bekijken voor meer informatie–
- Data Science versus Data Visualization
- Machine learning versus neuraal netwerk
- Begeleid leren versus diep leren
- Logistieke regressie in R