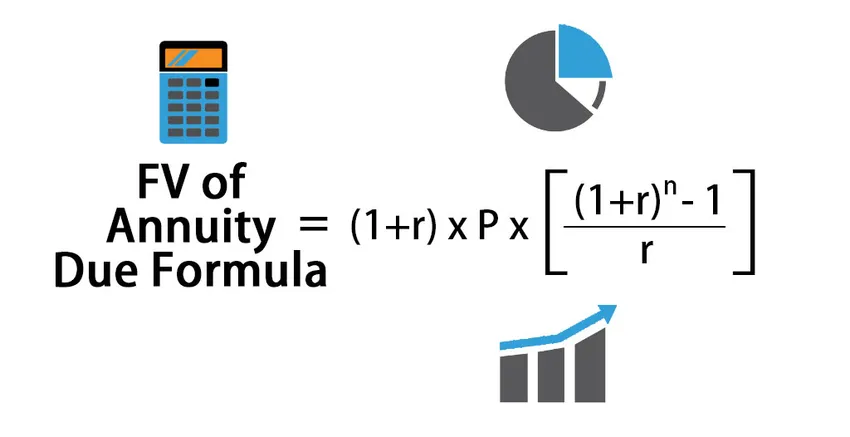
Toekomstige waarde van de te betalen lijfrente (inhoudsopgave)
- Toekomstige waarde van de te betalen lijfrente
- Voorbeelden van toekomstige waarde van de te betalen lijfrenteformule (met Excel-sjabloon)
- Toekomstige waarde van de formule voor te betalen lijfrente
Toekomstige waarde van de te betalen lijfrente
De formule voor het berekenen van de toekomstige waarde van de te betalen lijfrente:
FV of Annuity Due = (1+r) * P * (((1+r) n – 1) / r )
Waar,
- P = periodieke betaling
- R = Tarief per periode
- N = Aantal perioden
Voorbeelden van toekomstige waarde van de te betalen lijfrenteformule (met Excel-sjabloon)
Laten we een voorbeeld nemen om de berekening van de toekomstige waarde van de verschuldigde lijfrente op een betere manier te begrijpen.
U kunt deze toekomstige waarde van de te betalen lijfrente formule Excel-sjabloon hier downloaden - toekomstige waarde van de te betalen lijfrente formule Excel-sjabloonVoorbeeld 1
Laten we aannemen dat een Anand $ 10.000 per jaar heeft gestort en dat het effectieve tarief dat zijn account biedt 3% is. Nu wil Anand zijn toekomstige saldo na 5 jaar berekenen met de veronderstelling van de eerste storting vanaf vandaag.
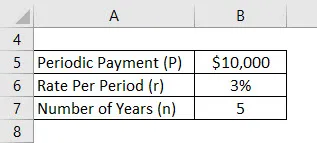
Oplossing:
De toekomstige waarde van de te betalen lijfrente wordt berekend met behulp van de onderstaande formule
FV van lijfrente verschuldigd = (1 + r) * P * (((1 + r) n - 1) / r)
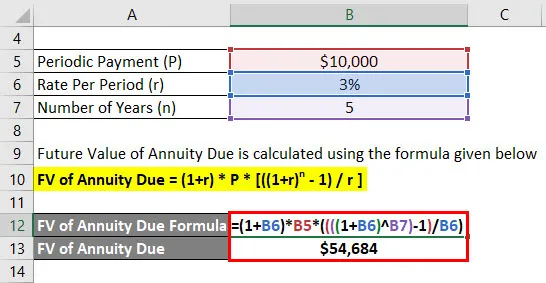
- FV van te betalen lijfrente = (1+ 3%) * $ 10.000 * ((((1 + 3%) 5) - 1) / 3%)
- FV van te betalen lijfrente = $ 54.684
Anand krijgt na 5 jaar $ 54.684 toekomstig saldo.
Voorbeeld 2
Laten we aannemen dat een Jagriti $ 8.000 per jaar heeft gestort en dat het effectieve tarief dat zijn account biedt 5% is. Nu wil Jagriti zijn toekomstige saldo na 5 jaar berekenen met de veronderstelling van de eerste storting vanaf vandaag.

Oplossing:
De toekomstige waarde van de te betalen lijfrente wordt berekend met behulp van de onderstaande formule
FV van lijfrente verschuldigd = (1 + r) * P * (((1 + r) n - 1) / r)
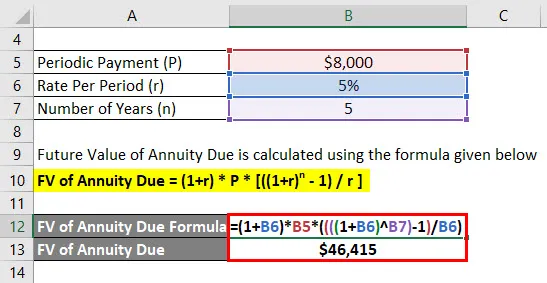
- FV van te betalen lijfrente = (1+ 5%) * $ 8.000 * ((((1 + 5%) 5) - 1) / 5%)
- FV van te betalen lijfrente = $ 46, 415
Jagriti krijgt na $ 5, 415 een toekomstig saldo.
Voorbeeld 3
Laten we aannemen dat een Anandriti $ 20.000 per jaar heeft gestort en dat het effectieve tarief dat zijn account biedt 2% is. Nu wil Anandriti zijn toekomstige saldo na 5 jaar berekenen met de veronderstelling van de eerste storting vanaf vandaag.
Oplossing:
De toekomstige waarde van de te betalen lijfrente wordt berekend met behulp van de onderstaande formule
FV van lijfrente verschuldigd = (1 + r) * P * (((1 + r) n - 1) / r)
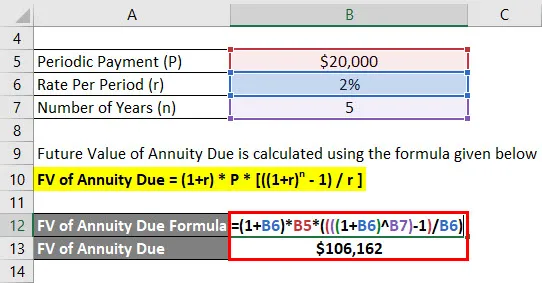
- FV van te betalen lijfrente = (1+ 2%) * $ 20.000 * ((((1 + 2%) 5) - 1) / 2%)
- FV van te betalen lijfrente = $ 1, 06, 162
Anandriti krijgt na 5 jaar $ 1, 06, 162 toekomstig saldo.
Uitleg
Om de eindwaarde te berekenen voor een reeks kasstromen of betalingen waarbij de eerste termijn direct wordt ontvangen, gebruiken we de toekomstige waarde van de verschuldigde rente. De eerste directe termijn of betaling onderscheidt de lijfrente als gevolg van de gewone lijfrente. Een onmiddellijke of onmiddellijke lijfrente wordt een verschuldigde lijfrente genoemd.
Het berekent de waarde van kasstromen in een toekomstige periode. Het gebruik van de FV van verschuldigde lijfrente is in reële situaties anders dan de contante waarde van een verschuldigde lijfrente. Stel bijvoorbeeld dat een bedrijf of een individu een lijfrente koopt en de eerste termijn vandaag heeft betaald. We kunnen het voorbeeld gebruiken om verder uit te leggen, stel dat een bedrijf of een individu een lijfrente van iemand wil kopen en vandaag de eerste betaling heeft gedaan. Om de te betalen prijs in deze situatie te berekenen, kunnen we de contante waarde van de annuïteitenformule gebruiken. Als we echter het resterende saldo willen berekenen na 5 jaar rente op de rekening te hebben opgeslagen en we hebben besloten om de eerste termijn vandaag te betalen, in dit geval wordt de toekomstige waarde van een annuïteit gebruikt. Te betalen lijfrente kan worden verklaard als een soort lijfrente waarbij kasstromen plaatsvinden aan het begin van elke periode. Vanwege het geavanceerde karakter van kasstromen, is elke kasstroom onderworpen aan het samengestelde effect voor elke extra periode in het geval dat deze wordt vergeleken met een gewone lijfrente. De toekomstige waarde van een gewone lijfrente is lager dan de toekomstige waarde van de lijfrente omdat de toekomstige waarde van de lijfrente een periodiek belang krijgt van de factor één plus.
Relevantie en gebruik van toekomstige waarde van verschuldigde lijfrente
Laten we de betekenis van toekomstige waarde en annuïteiten afzonderlijk begrijpen. De toekomstige waarde kan worden verklaard als de totale waarde voor een som contanten die in de toekomst op een specifieke datum moet worden betaald. En een te betalen lijfrente kan worden verklaard als de reeks betalingen die aan het begin van elke periode in regelmatige volgorde wordt gedaan. Daarom kan de toekomstige waarde van de te betalen annuïteit worden verklaard als de totale waarde op een specifieke datum in de toekomst voor een reeks systematische / periodieke betalingen waarbij de betalingen aan het begin van elke periode worden gedaan. Dit type transactie en een dergelijke stroom van betalingen kunnen worden gezien voor een begunstigde account van een pensioenplan. De totale waarde is het bedrag waarnaar de reeks betalingen in de toekomst zal groeien, aangezien een bepaald bedrag aan rente wordt verondersteld en de inkomsten geleidelijk toenemen gedurende een bepaalde periode. De berekening van de toekomstige waarde van een gewone lijfrente is identiek aan dit, maar het enige verschil is dat we een extra betalingstermijn toevoegen die in het begin wordt gemaakt.
Toekomstige waarde van de te betalen lijfrentecalculator
U kunt de volgende Future Value of Annuity Due Calculator gebruiken
| P | |
| r | |
| n | |
| Toekomstige waarde van de te betalen lijfrente | |
| Toekomstige waarde van de te betalen lijfrente = | (1 + r) * P * (((1 + r) n - 1) / r) |
| = | (1 +0) * 0 * (((1 +0) 0 -1) / 0) = 0 |
Aanbevolen artikelen
Dit is een leidraad geweest voor de Future Value of Annuity Due Formula. Hier bespreken we hoe de toekomstige waarde van de te betalen lijfrente te berekenen, samen met praktische voorbeelden. We bieden ook Future Value of Annuity Due-calculator met downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Gids voor tijd Waarde van geldformule
- Voorbeelden van Present Value Factor Formula
- Calculator voor informatieverhouding formule
- Formule voor de mate van hefboomwerking