
F-testformule (inhoudsopgave)
- Formule
- Voorbeelden
Wat is een F-testformule?
F-test is een statistische test die ons helpt te achterhalen of twee populatiesets met een normale verdeling van hun gegevenspunten dezelfde standaardafwijking of variaties hebben. Maar het allerbelangrijkste om de F-test uit te voeren, is dat de gegevenssets een normale verdeling moeten hebben. Dit wordt toegepast op de F-verdeling volgens de nulhypothese. F-test is een zeer cruciaal onderdeel van ANOVA (Analysis of Variance) en wordt berekend door verhoudingen van twee varianties van twee verschillende gegevenssets te nemen. Zoals we weten, geven varianties ons informatie over de spreiding van de gegevenspunten. F-test wordt ook gebruikt in verschillende tests zoals regressie-analyse, de Chow-test, enz.
Formule VOOR F-test:
Er is geen eenvoudige formule voor F-Test, maar het is een reeks stappen die we moeten volgen:
Stap 1: Om een F-test uit te voeren, moeten we eerst de nulhypothese en alternatieve hypothese definiëren. Deze worden gegeven door: -
- H0 (nulhypothese): variantie van de eerste gegevensset = variantie van een tweede gegevensset
- Ha: Variantie van de 1e dataset <Variantie van de 2e dataset (voor een lagere eenzijdige test)
- Ha: Variantie van de 1e dataset> Variantie van een 2e dataset (voor een bovenste eenzijdige test)
- Ha: Variantie van de eerste dataset ≠ Variantie van een 2e dataset (voor een tweezijdige test)
Stap 2: Het volgende dat we moeten doen, is dat we het niveau van significantie moeten achterhalen en vervolgens de vrijheidsgraden van zowel de teller als de noemer moeten bepalen. Dit helpt ons bij het bepalen van hun kritische waarden. Vrijheidsgraad is steekproefgrootte -1.
Stap 3: F-testformule:
F Value = Variance of 1 st Data Set / Variance of 2 nd Data Set
Stap 4: Zoek de F-kritieke waarde uit de F-tabel met een mate van vrijheid en een niveau van significantie.
Stap 5: Vergelijk deze twee waarden en als een kritische waarde kleiner is dan de F-waarde, kunt u de nulhypothese verwerpen.
Voorbeelden van F-testformule (met Excel-sjabloon)
Laten we een voorbeeld nemen om de berekening van F-Test op een betere manier te begrijpen.
U kunt deze F-TEST formule Excel-sjabloon hier downloaden - F-TEST formule Excel-sjabloonF-testformule - Voorbeeld # 1
Laten we zeggen dat we twee datasets A en B hebben die verschillende datapunten bevatten. Voer een F-test uit om te bepalen of we de nulhypothese op een significantieniveau van 1% kunnen verwerpen.
Gegevenssets:
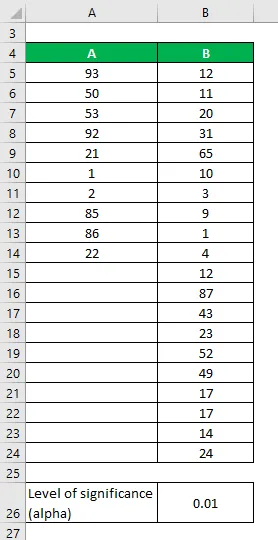
Oplossing:
Null-hypothese: variantie van A = variantie van B
Mate of Freedom wordt berekend als
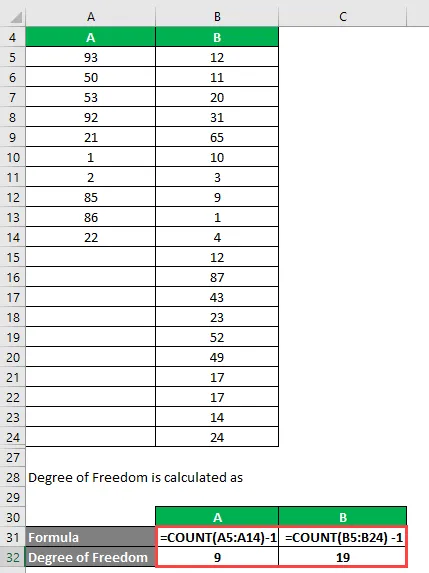
Graad van vrijheid
- Voor A = 10 - 1 = 9
- Voor B = 20 - 1 = 19
Variatie wordt berekend als:

- Variantie van A = 1385.61
- Variantie van B = 521.22
F Waarde wordt berekend met behulp van de onderstaande formule
F Waarde = Variantie van 1e dataset / Variantie van 2e dataset
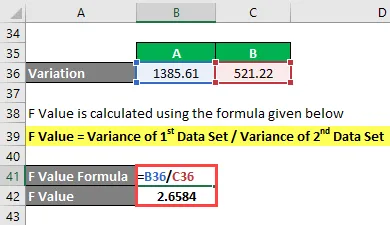
- F Waarde = 1385.61 / 521.22
- F Waarde = 2, 6584
F-tabel:
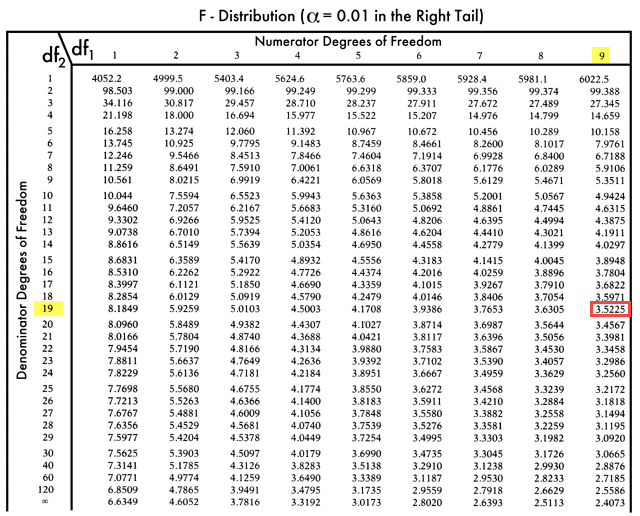
Dus F kritische waarde = 3.5225
Omdat F kritisch groter is dan de F waarde, kunnen we de nulhypothese niet verwerpen.
F-testformule - Voorbeeld # 2
Stel dat u in een onderzoeksbureau werkt en wilt dat het niveau van CO2-uitstoot van 2 verschillende sigarettenmerken en of ze aanzienlijk verschillen of niet. In uw analyse hebt u de volgende informatie verzameld:
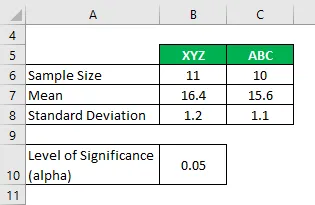
Oplossing:
Mate of Freedom wordt berekend als
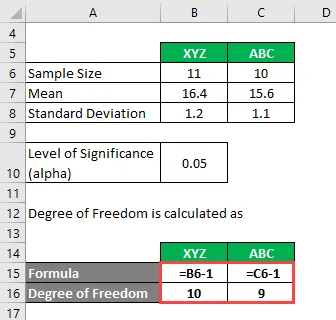
Graad van vrijheid
- Voor XYZ = 11 - 1 = 10
- Voor ABC = 10 - 1 = 9
Variatie wordt berekend als:
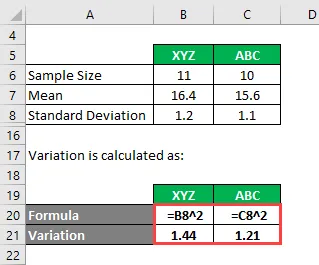
- Variantie van XYZ = 1, 2 2 = 1, 44
- Variantie van ABC = 1, 1 2 = 1, 21
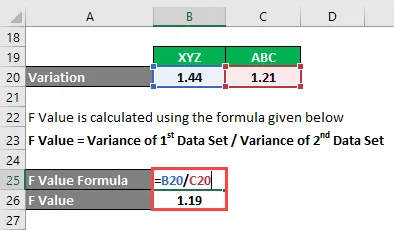
- F Waarde = 1, 44 / 1, 21
- F Waarde = 1, 19
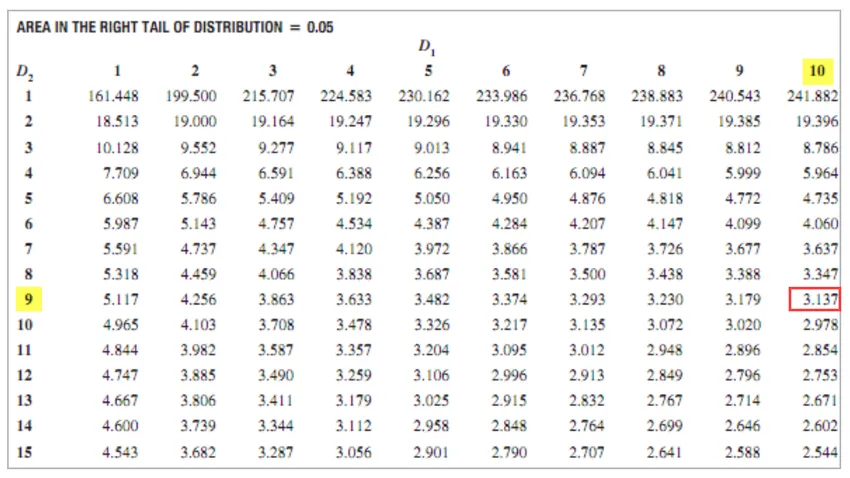
F Kritieke waarde = 3.137
Aangezien de F kritieke> F waarde, kan de nulhypothese niet worden verworpen.
Uitleg
In de bovenstaande voorbeelden hebben we de toepassing van F-Test gezien en hoe deze wordt uitgevoerd. Maar er is een stel veronderstellingen dat we moeten oppassen voordat we de F-test uitvoeren, anders krijgen we niet de vereiste resultaten:
- Het eerste is dat we bij het berekenen van de F-waarde altijd de teller met de hogere variantie moeten plaatsen. Dus als F = V1 / V2, moet V1> V2 zijn
- Als we 2 staarttests willen uitvoeren, moeten we het significantieniveau delen door 2 en dat is het juiste niveau om de kritieke waarde te vinden
- We gebruiken alleen variantie als de F-waardeberekening en als we standaardafwijkingen krijgen, zoals in voorbeeld 2, moeten ze worden gekwadrateerd om de variantie te vinden.
- Beide monsters moeten onafhankelijk van elkaar zijn en de steekproefgrootte moet kleiner zijn dan 30
- Populatiesets waaruit de monsters worden genomen, moeten normaal worden verdeeld
Dit zijn de belangrijkste parameters / veronderstelling waarmee rekening moet worden gehouden tijdens het uitvoeren van de F-test.
Relevantie en gebruik van F-testformule
F-test, zoals hierboven besproken, helpt ons om de gelijkheid van de twee populatievarianties te controleren. Dus als we twee onafhankelijke steekproeven hebben die uit een normale populatie zijn getrokken en we willen controleren of ze dezelfde variabiliteit hebben, gebruiken we de F-test. F-test heeft ook een grote relevantie in regressie-analyse en ook voor het testen van de significantie van R2. Kortom, F-Test is een zeer belangrijk hulpmiddel in de statistiek als we de variatie van twee of meer gegevenssets willen vergelijken. Maar je moet alle veronderstellingen in gedachten houden voordat je deze test uitvoert.
Aanbevolen artikelen
Dit is een leidraad geweest voor de F-testformule. Hier bespreken we hoe F-Test te berekenen, samen met praktische voorbeelden en een downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- T Distributieformule
- Formule voor prijsstelling van obligaties
- Percentage foutformule
- Berekening van de NOPAT-formule