
Inleiding tot invoeging Sorteren in JavaScript
Sorteren is een van de belangrijke concepten die programmeurs leren om hun reis in de informatica te beginnen, ongeacht de programmeertaal die is geselecteerd om te leren. Sorteren helpt ons om de doelgegevens waarnaar we willen zoeken op een snellere en gemakkelijke manier te vinden, door ze in oplopende of aflopende volgorde te sorteren.
Sorteeralgoritmen worden gebruikt om elementen te herschikken, waarbij een element een nummer of een string kan zijn. Er zijn veel soorten sorteeralgoritmen op basis van hun sorteermethode en de aanpak die ze volgen om de elementen te sorteren, en elk type heeft zijn voor- en nadelen.
In deze blog zullen we ons concentreren op invoegsortering, een veelgebruikte soort die gemakkelijk te begrijpen en te implementeren is.
Wat is invoegsortering in JavaScript?
Insertion Sort is een eenvoudig, gemakkelijk te begrijpen algoritme dat het beste werkt met een kleine gegevenslijst door elk element in de gegevenslijst één voor één van links naar rechts te sorteren. Het staat ook bekend als een vergelijkingssortering waarbij de huidige waarde wordt vergeleken met de andere waarden in dezelfde gegevenslijst die wordt gesorteerd. Het volgt een iteratieve benadering om elk element in de juiste volgorde in de gegevenslijst te plaatsen.
Hoe meer tijd het kost om een algoritme te sorteren, hoe slecht het presteert en dat een ander algoritme moet worden overwogen om de gegevens te sorteren. Invoegsortering heeft een tijdcomplexiteit van O (n²) of draait kwadratische tijd om de gegevenslijst in het ergste geval te sorteren. Dit is meestal niet erg effectief en mag niet worden gebruikt voor grote lijsten. Meestal presteert het echter beter dan geavanceerde algoritmen zoals quicksort of mergesort op kleinere lijsten.
Invoegsortering is meestal efficiënter dan andere kwadratische sorteeralgoritmen zoals bubbelsortering of selectiesortering. Het beste geval, tijd is O (n) of lineair, wat optreedt als de invoerarray al is gesorteerd. Gemiddeld loopt de invoegtijd nog steeds kwadratisch.
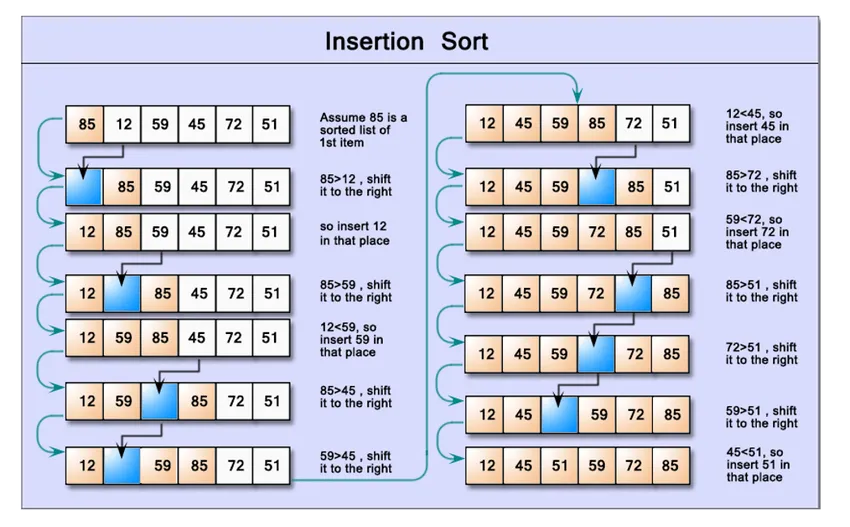
In het onderstaande voorbeeld zullen we een eenvoudige benadering op hoog niveau hebben om gegevens te sorteren die zijn opgeslagen in een matrixgegevensstructuur en de sorteermethode gebruiken om de gegevens te sorteren zonder algoritmen te implementeren.
Voorbeeld - Algoritme voor invoegsortering
Code:
// Declaring unsorted data and storing it in array data structure
var dataArray = (96, 5, 42, 1, 6, 37, 21) // Function - Insertion Sort Algo.
function insertSort(unsortedData) (
for (let i = 1; i < unsortedData.length; i++) (
let current = unsortedData(i);
let j;
for(j=i-1; j >= 0 && unsortedData(j) > current;j--) (
unsortedData(j + 1) = unsortedData(j) )
unsortedData(j + 1) = current;
)
return unsortedData;
)
// print sorted array
console.log(insertSort(dataArray));
Output:
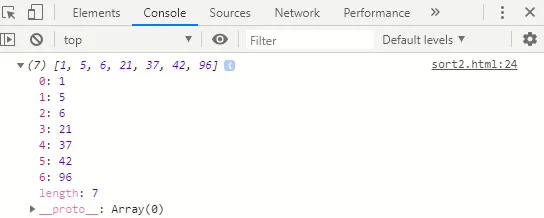
Verklaring: In het algoritme hebben we 2 voor lussen geïmplementeerd, de buitenste voor lus is om de matrixelementen te herhalen en de binnenste voor lus wordt gebruikt om de matrixelementen in oplopende volgorde van hun waarde te sorteren. De huidige variabele bevat de huidige waarde van de array en variabele j wordt ingesteld op één waarde minder dan de huidige indexpositie van de array. We controleren of het huidige element (huidig) kleiner is dan de matrixwaarde op de j - positie (unsortedData (j) ) en als het waar is, sorteren we die waarden.
Iteratie 1 - stroom (96): (96, 5, 42, 1, 6, 37, 21)
Iteratie 2 - stroom (5): (5, 96, 42, 1, 6, 37, 21)
Iteratie 3 - stroom (42): (5, 42, 96, 1, 6, 37, 21)
Iteratie 4 - stroom (1): (1, 5, 42, 96, 6, 37, 21)
Iteratie 5 - stroom (6): (1, 5, 6, 42, 96, 37, 21)
Iteratie 6 - stroom (37): (1, 5, 6, 37, 42, 96, 21)
Iteratie 7 - stroom (21): (1, 5, 6, 21, 37, 42, 96)
De buitenste voor lus-iteratie begint bij de 1e indexpositie, omdat we het kleinste element naar de linkerkant willen verplaatsen, dus we vergelijken of het huidige element kleiner is dan de elementen aan de linkerkant.
Typen sorteren
De soorten algoritmen die worden gebruikt voor het sorteren van gegevens omvatten de volgende concepten of ideeën in hun benadering van het sorteren van de gegevens:
- Vergelijking versus niet op vergelijking gebaseerde strategieën,
- Iteratieve versus recursieve implementatie,
- Verdeel en heers paradigma (dit of dat),
- Aanpak willekeurig maken.
Laten we een paar voorbeelden bekijken:
1. Samenvoegen sorteert een verdeel-en-verover-benadering om elementen in een array te sorteren.
2. Insertion Sort, Bubble Sort is een op vergelijking gebaseerde sortering.
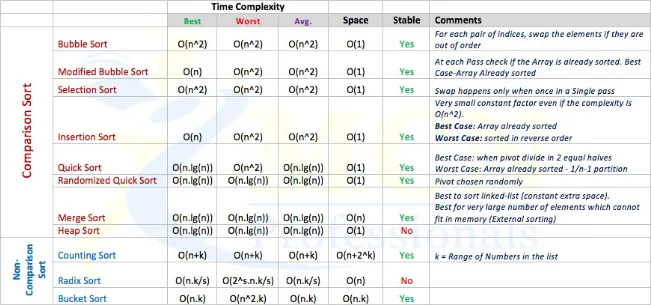
Wanneer gegevens worden gesorteerd, wordt het gemakkelijker om een optimale oplossing voor complexe problemen te bedenken. bijvoorbeeld,
- Zoeken naar een specifieke waarde,
- Het vinden van de minimum of maximum waarde,
- Testen op uniciteit en verwijderen van duplicaten,
- Tellen hoe vaak een specifieke waarde is verschenen, enz.
Conclusie
In dit artikel hebben we de definitie van invoegsortering en de tijdcomplexiteit ervan doorlopen en verschillende andere sorteeralgoritme-typen op basis van hun aanpak. Het bestuderen van verschillende sorteeralgoritmen helpt ons om te bepalen welke beter geschikt is in bepaalde omstandigheden of gebruiksscenario's die ons helpen om de gegevens sneller te sorteren.
Aanbevolen artikelen
Dit is een gids voor Invoegsortering in JavaScript. Hier bespreken we wat insertion sort in Javascript is en de typen daarvan met een voorbeeld. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Patronen in JavaScript
- Case Statement in JavaScript
- Voorwaardelijke verklaringen in JavaScript
- JavaScript-objecten
- Verschillende soorten loops met zijn voordelen