
Formule van variatiecoëfficiënt (inhoudsopgave)
- Formule
- Voorbeelden
Wat is de formule van de variatiecoëfficiënt?
In statistieken is de variatiecoëfficiënt ook wel CV genoemd een hulpmiddel dat ons helpt te bepalen hoe datapunten in een dataset rond het gemiddelde worden verdeeld. In principe worden eerst alle gegevenspunten uitgezet en vervolgens wordt de variatiecoëfficiënt gebruikt om de spreiding van die punten ten opzichte van elkaar en het gemiddelde te meten. Dus het helpt ons bij het begrijpen van de gegevens en ook om het patroon te zien dat het vormt. Het wordt berekend als een verhouding van de standaarddeviatie van de gegevensverzameling tot gemiddelde waarde. Een hogere variatiecoëfficiënt betekent dat er een grotere spreiding van gegevens is rond het gemiddelde. Evenzo, hoe lager de waarde van de variatiecoëfficiënt, hoe kleiner de spreiding en hoe nauwkeuriger de resultaten. Zelfs als het gemiddelde van twee gegevensreeksen aanzienlijk verschilt, is de variatiecoëfficiënt zeer nuttig om de mate van variatie van de ene gegevensreeks met de andere te vergelijken.
Formule voor de variatiecoëfficiënt wordt gegeven door:
Coefficient of Variation = Standard Deviation / Mean
Stappen om de variatiecoëfficiënt te berekenen:
Stap 1: Bereken het gemiddelde van de gegevensset. Gemiddelde is het gemiddelde van alle waarden en kan worden berekend door de som van alle waarden te nemen en deze vervolgens te delen door een aantal gegevenspunten.
Stap 2: Bereken vervolgens de standaardafwijking van de gegevensset. Dat is een beetje tijdrovend proces. Standaardafwijking kan worden berekend als: √ (Σ (X i - X m ) 2 / (n - 1)) . X i is het ie gegevenspunt en X m is het gemiddelde van de gegevensset. Als alternatief kunnen we ook de standaarddeviatie vinden in excel met de STDEV.S () -functie.
Stap 3: Deel de standaarddeviatie door gemiddelde om de variatiecoëfficiënt te krijgen.
Voorbeelden van de formule van de variatiecoëfficiënt (met Excel-sjabloon)
Laten we een voorbeeld nemen om de berekening van de variatiecoëfficiënt beter te begrijpen.
U kunt deze coëfficiënt van variatieformule Excel-sjabloon hier downloaden - Coëfficiënt van variatieformule Excel-sjabloonFormule van variatiecoëfficiënt - Voorbeeld # 1
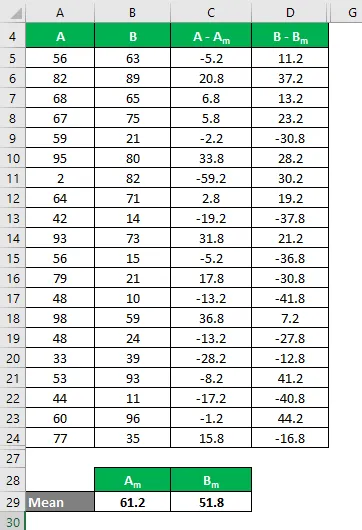
Laten we zeggen dat we twee gegevenssets A en B hebben en elk 20 willekeurige gegevenspunten bevat. Bereken de variatiecoëfficiënt voor de gegevensset X & Y.
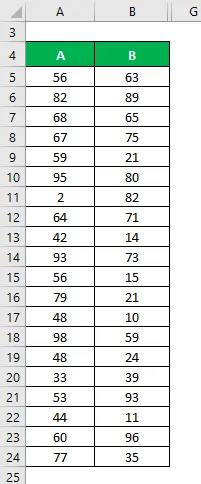
Oplossing:
Gemiddelde wordt berekend als:
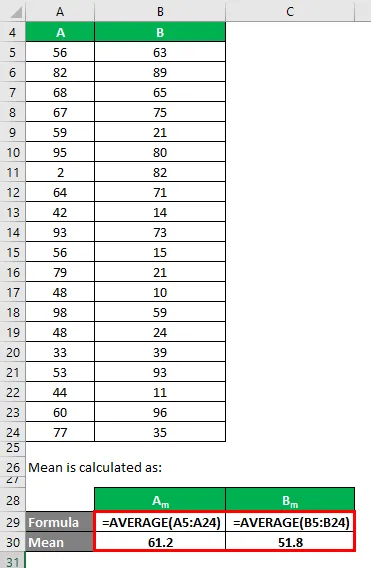
- Gemiddelde van gegevensset A = 61.2
- Gemiddelde van gegevensset B = 51, 8
Nu moeten we het verschil tussen de gegevenspunten en de gemiddelde waarde berekenen.
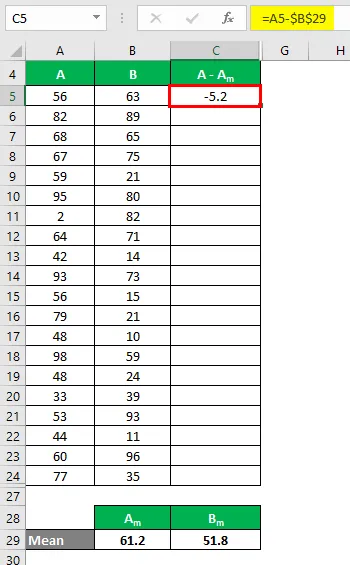
Bereken op dezelfde manier voor alle waarden van de gegevensset A.
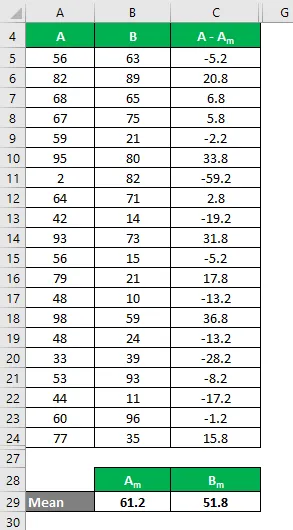
Bereken op dezelfde manier voor alle waarden van de gegevensset B.
Bereken het kwadraat van het verschil voor zowel de datasets A als B.
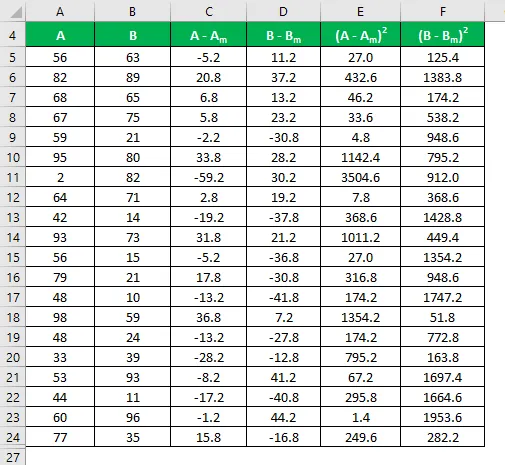
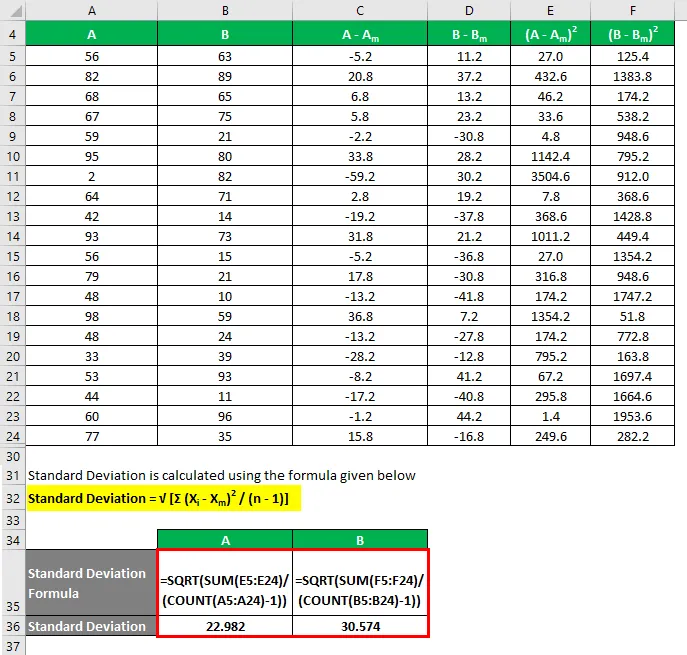
Standaardafwijking wordt berekend met behulp van de onderstaande formule
Standaardafwijking = √ (Σ (X i - X m ) 2 / (n - 1))
Variatiecoëfficiënt wordt berekend met behulp van de onderstaande formule
Variatiecoëfficiënt = standaardafwijking / gemiddelde
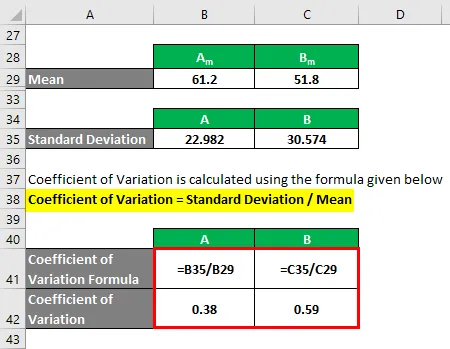
- Variatiecoëfficiënt A = 22.982 / 61.2 = 0.38
- Variatiecoëfficiënt B = 30.574 / 51.8 = 0, 59
Dus als je hier ziet, heeft B een hogere variatiecoëfficiënt dan A, wat betekent dat gegevenspunten van B meer verspreid zijn dan A.
Formule van variatiecoëfficiënt - Voorbeeld # 2
Stel dat u een zeer risicomijdende belegger bent en dat u geld op de aandelenmarkt wilt beleggen. Omdat uw risicobereidheid laag is, wilt u beleggen in veilige aandelen met een lagere standaardafwijking en variatiecoëfficiënt. U heeft 3 aandelen genomineerd op basis van hun fundamentele en technische informatie en wilt 2 aandelen kiezen. U hebt ook informatie verzameld over hun historische rendementen van de afgelopen 15 jaar.
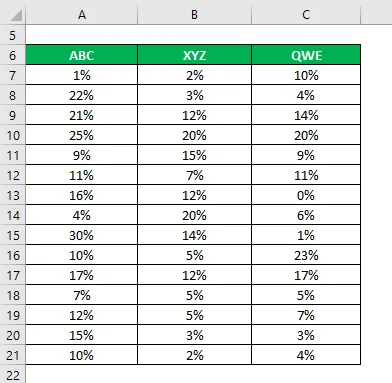
Oplossing:
Gemiddelde wordt berekend als:
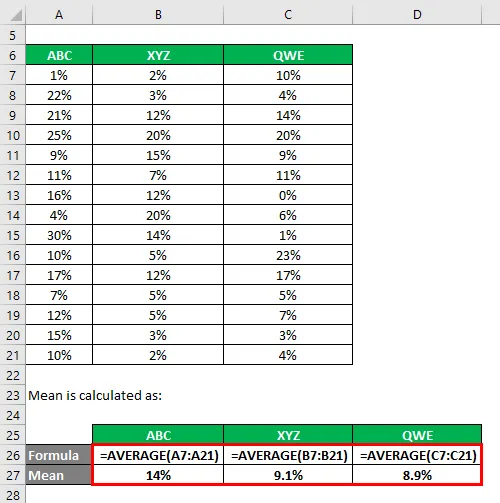
Standaardafwijking wordt berekend met de Excel-formule
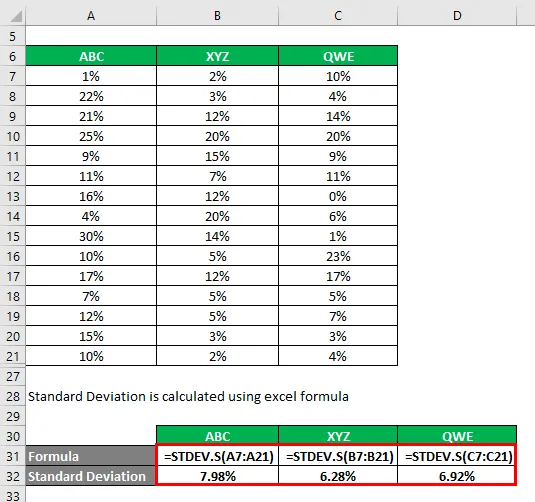
Variatiecoëfficiënt wordt berekend met behulp van de onderstaande formule
Variatiecoëfficiënt = standaardafwijking / gemiddelde
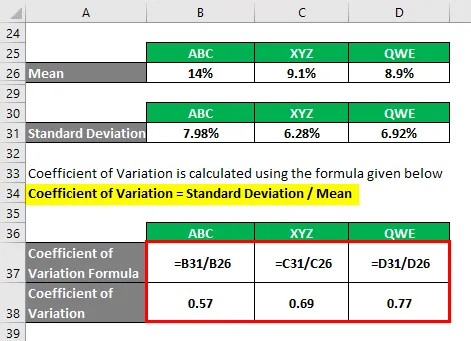
- Variatiecoëfficiënt ABC = 7, 98% / 14% = 0, 57
- Variatiecoëfficiënt XYZ = 6, 28% / 9, 1% = 0, 69
- Variatiecoëfficiënt QWE = 6, 92% / 8, 9% = 0, 77
Op basis van de informatie kiest u aandelen ABC en XYZ om te beleggen, omdat ze de laagste variatiecoëfficiënt hebben.
Uitleg
Aangezien de variatiecoëfficiënt een maat voor het risico is, helpt het bij het meten van de volatiliteit van de koersen van aandelen en andere financiële instrumenten. Het helpt beleggers en analisten ook bij het vergelijken van de risico's die verbonden zijn aan verschillende potentiële investeringen.
Variatiecoëfficiënt is vergelijkbaar met standaardafwijking, maar een standaardafwijking van twee variabelen kan niet nuttig worden vergeleken. Maar het gebruik van standaarddeviatie en het gemiddelde maakt de relatieve vergelijking zinvoller. Er is ook een beperking van de variatiecoëfficiënt. Stel dat het gemiddelde van een gegevensset nul is. In dat geval wordt deze tool niet meer effectief. Niet alleen dit, als we een gegevensset hebben die veel positieve en negatieve waarden heeft, wordt de variatiecoëfficiënt erg problematisch. Het is dus alleen nuttiger bij gegevenssets met hetzelfde plusteken.
Relevantie en gebruik van de formule van de variatiecoëfficiënt
Variatiecoëfficiënt is relevant in veel andere velden dan statistieken. Op het gebied van financiën is de variatiecoëfficiënt bijvoorbeeld een maat voor het risico. Het is vergelijkbaar met standaarddeviatie, omdat dat ook wordt gebruikt als een maat voor het risico, maar het verschil is dat de variatiecoëfficiënt een betere indicator is voor het relatieve risico. Laten we bijvoorbeeld zeggen A's verwachte rendement van 15% en B's verwachte rendement van 10% en A heeft een standaarddeviatie van 10%, terwijl B een standaarddeviatie van 5% heeft. Om een betere investering te kiezen, kan de variatiecoëfficiënt worden gebruikt. Dus de variatiecoëfficiënt van A is 10/15 = 0, 666 en de variatiecoëfficiënt van B is 5/10 = 0, 5. Dus B is een betere investering dan A.
Aanbevolen artikelen
Dit is een leidraad geweest voor de Coefficient of Variation Formula. Hier bespreken we hoe de variatiecoëfficiënt met behulp van de formule wordt berekend, samen met praktische voorbeelden en een downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Wat is Adjusted R Squared Formula?
- Voorbeelden van bepalingscoëfficiëntformule
- Hoe de correlatiecoëfficiënt berekenen met behulp van formule?
- Covariantie-formule met Excel-sjabloon