Complexe nummers in MATLAB - Hoe een complex nummer te genereren?

Inleiding tot complexe getallen in MATLAB

Complexe getallen zijn de combinatie van reële getallen en denkbeeldige getallen in de vorm van p + qi waarbij p en q de reële getallen zijn en i het denkbeeldige getal is. Een denkbeeldig getal wordt gedefinieerd waarbij i het resultaat is van een vergelijking a 2 = -1. We kunnen i of j gebruiken om de denkbeeldige eenheden aan te duiden. Omdat complexe getallen worden gebruikt in wiskundige berekeningen en Matlab voornamelijk wordt gebruikt om wiskundige berekeningen uit te voeren. Complexe getallen vormen dus een belangrijk onderdeel van het leren van Matlab.

Complexe nummers genereren in MATLAB

Complexe nummers kunnen in Matlab worden gemaakt of gedeclareerd met behulp van een 'complexe' functie. We kunnen ook complexe getallen maken door de vierkantswortel van een negatief getal te vinden. In Matlab kunnen we i of j gebruiken om het imaginaire deel van het complexe getal aan te duiden.

Voorbeelden

X = 4 + 5i

Hier is X een complex getal dat 2 delen bevat, dwz een reëel en denkbeeldig deel. 4 is het echte deel en 5 is het denkbeeldige deel. We kunnen de echte en denkbeeldige delen vinden met behulp van functies in Matlab.

a = real (X) = 4 (dit geeft het reële deel van het complexe getal)
b = imag (X) = 5 (dit geeft het imaginaire deel van het complexe getal)
complex (6, 7) = 6 + 7i (deze functie wordt gebruikt om een complex nummer te maken)

We kunnen ook complexe matrices in Matlab maken die ook met behulp van de complexe functies kunnen worden gedeclareerd.

a = complex (x, y)

Er zijn bepaalde voorwaarden voor x en y die we moeten volgen zoals x en y mag niet enkel of dubbel zijn. Een complexe scalar kan worden gemaakt als twee ingangen scalair van aard zijn, zoals

X = complex (5, 3)
X = 5.0000 + 3.0000i

Evenzo kan een complexe vector worden gemaakt als we twee ingangen als vectoren hebben.

X = uint8 ((4, 5, 6, 7));
Y = uint8 ((3, 5, 1, 2));
a = complex (X, Y)

4 + 3i

5 + 5i

6 + 1i

7 + 2i

We kunnen een complex getal maken met slechts één scalair,

X = complex (10)
X = 10.0000 + 0.0000i

Er zijn bepaalde voorwaarden waaraan de invoer- en uitvoerargumenten moeten voldoen,

De invoerargumenten bevatten echte en denkbeeldige delen zoals x elke y. x en y moeten scalair, vector, multidimensionale array of matrix in MATLAB zijn. x en y moeten hetzelfde zijn. Ze moeten van hetzelfde gegevenstype zijn, maar er zijn enkele uitzonderingen, zoals dubbel kan worden gebruikt met enkel en geheel getal kan worden gecombineerd met een dubbel die scalair is.

De uitvoer van de array kan een vector-, scalaire, matrix- of multidimensionale array zijn, afhankelijk van de invoerargumenten. De grootte van de uitvoer moet hetzelfde zijn als de invoer. Als de invoerargumenten van verschillende gegevenstypen zijn dan de uitvoer wordt bepaald door,

Als een van de invoerargumenten één van aard is, moet de uitvoer ook single zijn.
Als een van de invoerargumenten een geheel getal van aard is, moet de uitvoer van een geheel gegevenstype zijn.

We kunnen controleren of de matrix echt of denkbeeldig is door de isreal-functie te gebruiken.

Code:

X = (2+i, 1); Isreal(X)

Output:

Code:

Isreal (X (2))

Output:

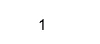
Om de echte en imaginaire delen te extraheren, kunnen we echte en imag-functies in Matlab gebruiken,

Code:

real(X)

Output:

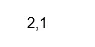
Code:

imag(X)

Output:

Bewerkingen en functies van complexe getallen in MATLAB

Er zijn verschillende bewerkingen en functies die kunnen worden uitgevoerd met behulp van complexe getallen zoals in Matlab

abs: deze functie wordt gebruikt om de modulus van elk complex getal in de vorm van p + qi te vinden. abs (2 + 3i) = vierkantswortel van (2 2 + 3 2) = (13) 0.5
hoek: om de fasehoek van het complexe getal te vinden.

Er zijn bepaalde tips die moeten worden gevolgd voor het goed functioneren van complexe getallen in Matlab zoals,

We moeten vermijden dat i en j worden gebruikt als onderdeel van variabelenamen, omdat deze worden gebruikt om de denkbeeldige delen van het complexe getal aan te duiden.
We moeten het gebruik van j of i vermijden als het denkbeeldige deel 1 is. In plaats daarvan kunnen we 1j of 1i gebruiken.
We kunnen een complexe functie in Matlab maken wanneer i en j in een deel als variabelenamen worden gebruikt, invoerargumenten niet van het enkele of dubbele type zijn en het denkbeeldige deel nul is.

Conclusie

Complexe nummers worden gebruikt op wiskundig of technisch gebied. Veel real-life of praktische toepassingen kunnen worden beschreven met behulp van het denkbeeldige deel van complexe getallen. Het is dus belangrijk om het gebruik en de toepassingen van complexe getallen op verschillende platforms te begrijpen, vooral als u te maken hebt met een fysiek of wiskundig domein.

Aanbevolen artikelen

Dit is een gids voor complexe getallen in MATLAB. Hier bespreken we de introductie en complexe nummergeneratie in Matlab inclusief de voorbeelden met bediening en functie. U kunt ook de volgende artikelen bekijken voor meer informatie-