
Verschil tussen Z-score en T-score
Z-score is een conversie van ruwe gegevens naar een standaardscore, wanneer de conversie is gebaseerd op het populatiegemiddelde en de populatiestandaarddeviatie. Wanneer een volledige gegevensset bij ons beschikbaar is, kunnen we de Z-score berekenen. Z-score is de aftrekking van het populatiegemiddelde van de ruwe score en deelt het resultaat vervolgens met de standaarddeviatie van de populatie. T-score is een conversie van ruwe gegevens naar de standaardscore wanneer de conversie is gebaseerd op het steekproefgemiddelde en de standaardafwijking van de steekproef. Als de populatiegegevensset niet beschikbaar is, moeten we enkele steekproefgegevens verzamelen om het steekproefgemiddelde en de populatiestandaardafwijking te berekenen.
Z score
Bij een normale distributie, waar volledige gegevens beschikbaar zijn, bevindt deze zich op een afstand van het gemiddelde. De formule is zoals hieronder gegeven,
Z= (x-μ)/σ
Waar,
X = individuele onbewerkte gegevens
μ = Populatiegemiddelde
σ = standaarddeviatie van de bevolking
T-score
T-score is de aftrekking van de individuele standaarddeviatie van het individuele gemiddelde en deelt het resultaat vervolgens met het standaardresultaat van de standaarddeviatie van de steekproef vermenigvuldigd met de steekproefgrootte. De formule is zoals hieronder gegeven,
t = ((- μ)/s)*
= steekproefgemiddelde
μ = Populatiegemiddelde
s = steekproef standaardafwijking
n = steekproefgrootte
Laten we een voorbeeld nemen om hetzelfde beter te begrijpen:
In een paper zijn er 3 onderverdelingen: I, II en III. Laat het aantal studenten dat ik heb geantwoord correct 25% zijn, dwz 75% kan dit niet correct beantwoorden. Evenzo, laat 10% en 20% door het aantal mensen dat sectie II en III correct heeft beantwoord, dus 90% en 80% hebben echter sectie II en III gevonden. We nemen aan dat het vermogen gemeten door deze drie items hetzelfde is en normaal wordt verdeeld,
De score voor elke student in een klas wordt gebruikt om het gemiddelde van de scores te berekenen dat gelijk is aan 50 en een standaarddeviatie van 10. We kunnen de Z-score berekenen met de score van 50 als (50-50) / 10 = 0
We kunnen interpreteren dat de studentenscore 0 afstand is (in eenheden van standaarddeviaties) van het gemiddelde, zodat de student gemiddeld scoort.
Als de score 60 is, is de Z-score (60-50) / 10 = 1
We kunnen interpreteren dat de student bovengemiddeld scoort - een afstand van 1 standaarddeviatie boven het gemiddelde.
Head to Head-vergelijking tussen de Z-score en de T-score (infographics)
Hieronder staat het top 9-verschil tussen de Z-score en de T-score 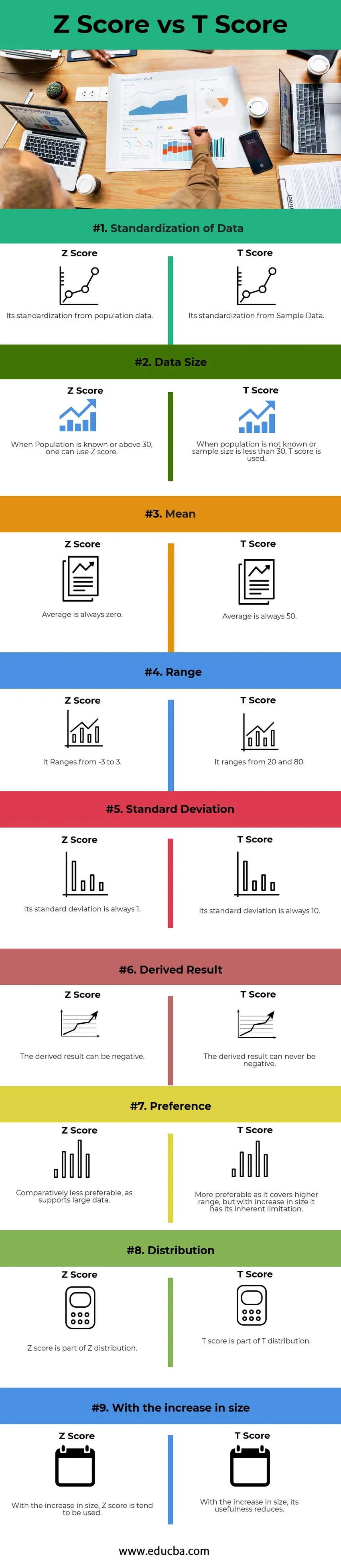
Belangrijkste verschillen tussen de Z-score en de T-score
Laten we enkele van de belangrijkste verschillen tussen de Z-score en de T-score bespreken
- Z-score is de standaardisatie van de populatie onbewerkte gegevens of meer dan 30 steekproefgegevens naar standaardscore, terwijl T-score standaardisatie is van de steekproefgegevens van minder dan 30 gegevens naar standaardscore
- Z-score varieert van -3 tot 3, terwijl de T-score varieert van 20 tot 80.
- Naarmate de gegevens groter worden, is distributie meestal Z-distributie. Beide Z-scores versus T-scores zijn onderdeel van een normale verdeling, maar op basis van de grootte verschillen ze van elkaar
- In de praktijk wordt de Z-score op grote schaal gebruikt in beursgegevens en om de kansen te controleren dat een bedrijf failliet gaat, terwijl de T-score op grote schaal wordt gebruikt bij het controleren van botmineraaldichtheid en fractuurrisicobeoordelingen
Z-score versus T-score Vergelijkingstabel
Laten we eens kijken naar de top 9-vergelijking tussen de Z-score en de T-score
| Sorry. Nee. | Punten van vergelijking | Z Score | T-score |
| 1 | Standaardisatie van gegevens | De standaardisatie van populatiegegevens | De standaardisatie van voorbeeldgegevens |
| 2 | Gegevensgrootte | Wanneer Populatie bekend is of boven de 30, kan men de Z-score gebruiken | Als de populatie niet bekend is of de steekproefgrootte kleiner is dan 30, wordt de T-score gebruikt. |
| 3 | Gemeen | Een gemiddelde is altijd nul. | Een gemiddelde is altijd 50. |
| 4 | reeks | Het varieert van -3 tot 3. | Het varieert van 20 en 80. |
| 5 | Standaardafwijking | De standaardafwijking is altijd 1 | De standaardafwijking is altijd 10 |
| 6 | Afgeleide resultaten | Het afgeleide resultaat kan negatief zijn | Het afgeleide resultaat kan nooit negatief zijn |
| 7 | Voorkeur | Relatief minder de voorkeur, omdat het grote gegevens ondersteunt | Meer de voorkeur omdat het een hoger bereik bestrijkt, maar met een toename in grootte heeft het zijn inherente beperking |
| 8 | Distributie | Z-score maakt deel uit van de Z-distributie | T-score maakt deel uit van T-distributie |
| 9 | Met de toename van de grootte | Met de toename in grootte wordt de Z-score meestal gebruikt | Met de toename in grootte neemt het nut ervan af. |
Conclusie
Zowel de Z-score als de T-score maakt deel uit van de hypothesetests onder de normale verdeling. Als u een reeks meetscores hebt voor verschillende metingen met behulp van Z-scores, kunt u zien hoe de scores in hun verdelingen worden geplaatst. Dan kun je ze vergelijken. Standaardisatie van scores is een veel gebruikte procedure op het gebied van onderzoek en planning, aangezien ze helpen bij het vergelijken van verschillende testscores. Standaardisatie van scores voordat ze worden gecombineerd, helpt een onderzoeker om betere en vergelijkbare resultaten te krijgen.
Aanbevolen artikelen
Dit is een leidraad geweest voor het grootste verschil tussen de Z-score en de T-score. Hier bespreken we ook de belangrijkste verschillen tussen de Z-score en de T-score met infographics en vergelijkingstabel. U kunt ook een kijkje nemen in de volgende artikelen voor meer informatie-
- Financiën versus economie - Top verschil
- Tekort versus schuld - welke is beter
- Activa-inkoop versus aandelenaankoop
- Geldmarkt versus kapitaalmarkt
- Overzicht van Altman Z Score