
Variantie-analyseformule (inhoudsopgave)
- Formule
- Voorbeelden
Wat is de variantie-analyseformule?
Variantieanalyse is een vrij belangrijke formule die wordt gebruikt bij portefeuillebeheer en andere financiële en bedrijfsanalyses. De kwantitatieve formule kan worden gemeten als het verschil tussen geplande en werkelijke aantallen. De formule wordt veel gebruikt in kostenanalyses om de variantie tussen de geplande of de standaardkosten versus de werkelijke kosten te controleren. De analyse helpt het management om de operationele prestaties van het bedrijf te controleren.
Formule voor variantieanalyse wordt hieronder gegeven
Variance = (X – µ) 2 / N
- X staat voor de waarde van het individuele gegevenspunt
- µ staat voor het gemiddelde of het gemiddelde van het individuele gegevenspunt
- N staat voor het aantal individuele datapunten in een gegeven array
Variantie-analyseformule wordt gebruikt in een opzet en variantie van de waarschijnlijkheidsverdeling, die ook worden gedefinieerd als de maat voor het risico op basis van een gemiddeld gemiddelde. Variantie geeft ook weer hoeveel de belegger in staat is het risico te nemen bij de aankoop van een specifiek effect.
Voorbeelden van formule voor variantieanalyse (met Excel-sjabloon)
Laten we een voorbeeld nemen om de berekening van de variantieanalyse beter te begrijpen.
U kunt deze variantieanalyse-formule Excel-sjabloon hier downloaden - Variantieanalyse-formule Excel-sjabloonVariantie-analyseformule - Voorbeeld # 1
Beschouw een gegevensset met de volgende observaties 2, 3, 6, 6, 7, 2, 1, 2, 8. We moeten de variantieanalyse berekenen.
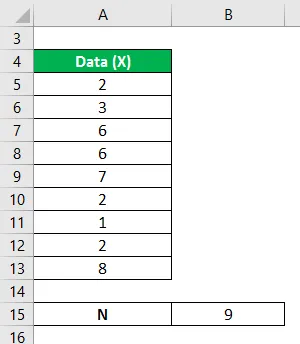
De oplossing voor het volgende probleem kan worden opgelost door de volgende stappen te nemen:
Gemiddelde wordt berekend als:

Nu moeten we het verschil tussen de gegevenspunten en de gemiddelde waarde berekenen.
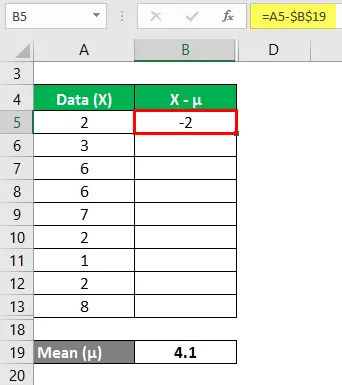
Vergelijk op dezelfde manier voor alle waarden van de gegevensset.
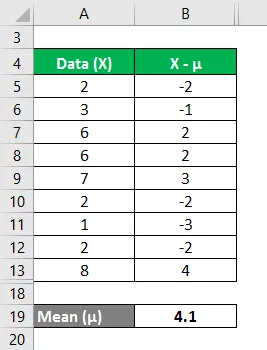
Bereken het kwadraat van het verschil tussen gegevenspunten en de gemiddelde waarde.
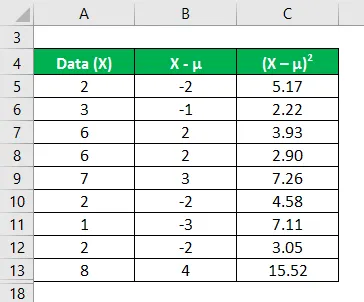
Variantieanalyse wordt berekend met behulp van de onderstaande formule
Variantie = (X - µ) 2 / N
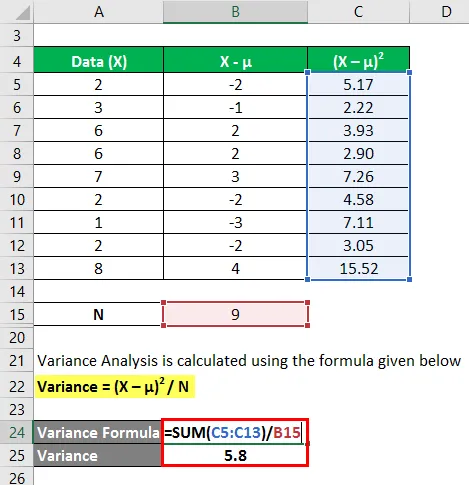
In de eerste stap hebben we het gemiddelde berekend door optelling (2 + 3 + 6 + 6 + 7 + 2 + 1 + 2 + 8) / aantal waarnemingen dat ons een gemiddelde van 4, 1 geeft. Vervolgens hebben we in kolom 2 het verschil tussen de gegevenspunten en de gemiddelde waarde berekend en elke waarde afzonderlijk gekwadrateerd. Daarna geeft het opsommen van kolom C en delen door het aantal waarnemingen ons de variantie van 5.8.
Variantie-analyseformule - Voorbeeld # 2
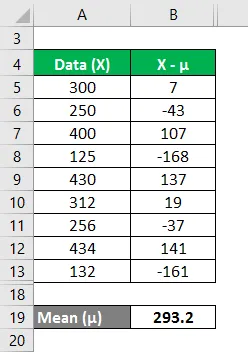
De hoogten van de honden in een gegeven set van een willekeurige variabele zijn 300 mm, 250 mm, 400 mm, 125 mm, 430 mm, 312 mm, 256 mm, 434 mm en 132 mm. Bereken de variantieanalyse van de gegevensset uit het gemiddelde.
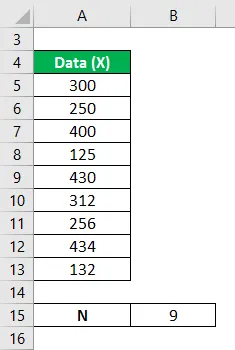
De oplossing voor het volgende probleem kan worden opgelost door de volgende stappen te nemen:
Gemiddelde wordt berekend als:
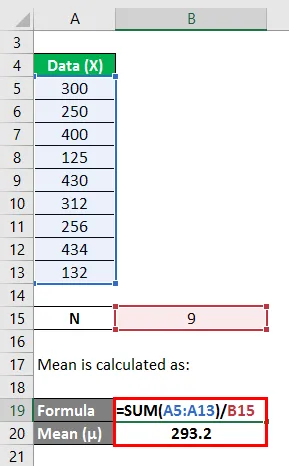
Nu moeten we het verschil tussen de gegevenspunten en de gemiddelde waarde berekenen.
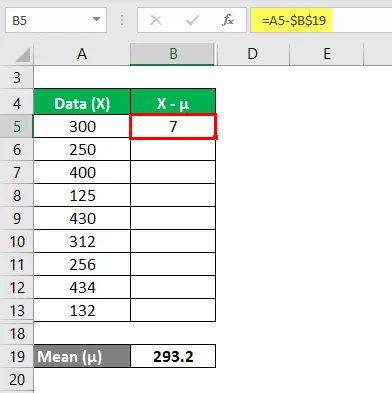
Vergelijk op dezelfde manier voor alle waarden van de gegevensset.
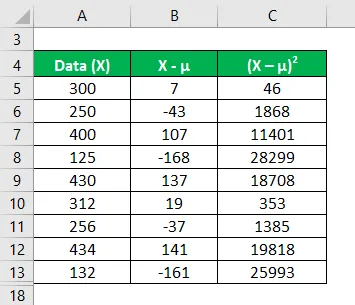
Bereken het kwadraat van het verschil tussen gegevenspunten en de gemiddelde waarde.
Variantieanalyse wordt berekend met behulp van de onderstaande formule
Variantie = (X - µ) 2 / N
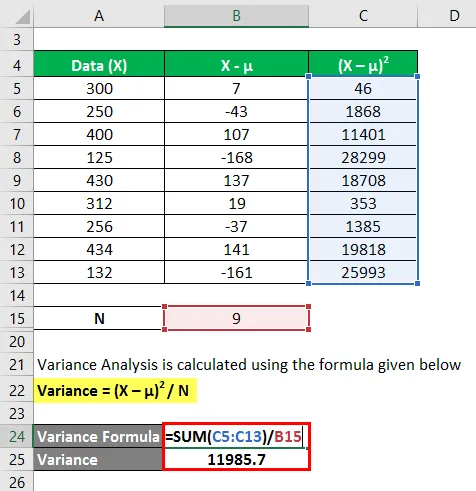
In de eerste stap hebben we het gemiddelde berekend door optelling (300 + 250 + 400 + 125 + 430 + 312 + 256 + 434 + 132) / aantal observaties, wat ons een gemiddelde van 293, 2 geeft. Vervolgens hebben we in kolom 2 het verschil tussen de gegevenspunten en de gemiddelde waarde berekend en elke waarde afzonderlijk gekwadrateerd. Na het samenvatten van kolom C en delen door het aantal observaties geeft ons de variantie van 11985.7.
Variantie-analyseformule - Voorbeeld # 3
De cijfers behaald door de studenten geselecteerd uit een grote steekproef van 100 studenten zijn 12, 15, 18, 24, 36, 10. Bereken de variantieanalyse van de gegevens van het gemiddelde.
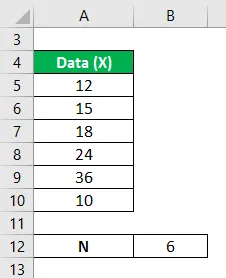
De oplossing voor het volgende probleem kan worden opgelost door de volgende stappen te nemen:
Gemiddelde wordt berekend als:

Nu moeten we het verschil tussen de gegevenspunten en de gemiddelde waarde berekenen.
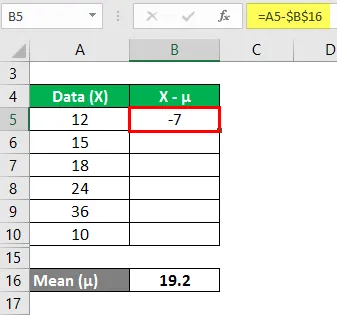
Vergelijk op dezelfde manier voor alle waarden van de gegevensset.
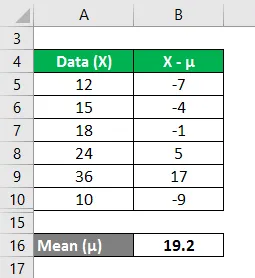
Bereken het kwadraat van het verschil tussen gegevenspunten en de gemiddelde waarde.
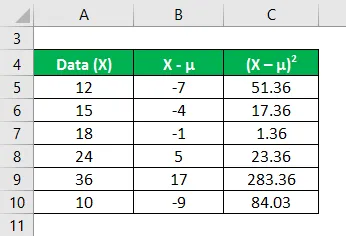
Variantieanalyse wordt berekend met behulp van de onderstaande formule
Variantie = (X - µ) 2 / N
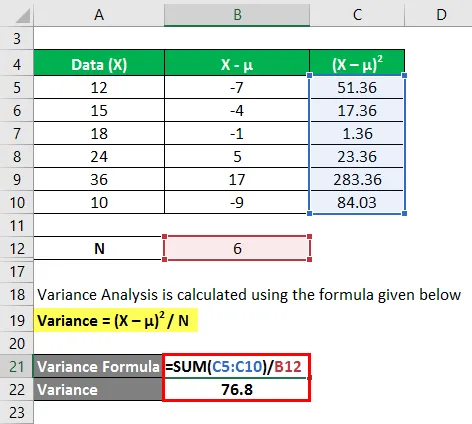
In de eerste stap hebben we het gemiddelde berekend door optelling (12 + 15 + 18 + 24 + 36 + 10) / aantal waarnemingen dat ons een gemiddelde van 19, 2 geeft. Vervolgens hebben we in kolom 2 het verschil tussen de gegevenspunten en de gemiddelde waarde berekend en elke waarde afzonderlijk gekwadrateerd. Daarna geeft het opsommen van kolom C en delen door het aantal waarnemingen ons de variantie van 76.8
Uitleg
De variantieanalyseformule wordt berekend met behulp van de volgende stappen: -
Stap 1: Bereken het gemiddelde van het aantal waarnemingen dat aanwezig is in de gegevensmatrix. Dit kunnen we berekenen met een eenvoudige gemiddelde formule die de som is van alle waarnemingen gedeeld door het aantal waarnemingen.
Stap 2: Na het berekenen van het gemiddelde van de waarnemingen wordt elke waarneming afgetrokken van het gemiddelde om de afwijking van elke waarneming van het gemiddelde te berekenen.
Stap 3: Het verschil van elke waarneming wordt vervolgens opgeteld en gekwadrateerd om de negatief-positieve signalen te vermijden en wordt vervolgens gedeeld door het aantal waarnemingen.
Relevantie en gebruik van de formule voor variantieanalyse
De variantieanalyse kan op de volgende gebieden worden gebruikt: -
- Portfolio Management
- Berekening van aandelen- en portefeuillerendement
- Budget versus werkelijke kostenvergelijking die zeer vaak in het bedrijf wordt gebruikt
- Voorspelling van kosten en opbrengsten
- Materialiteit
- Relaties tussen twee variabelen
Aanbevolen artikelen
Dit is een leidraad geweest voor de formule voor variantieanalyse. Hier bespreken we hoe de variantieanalyse te berekenen, samen met praktische voorbeelden en een downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Percentage foutformule met calculator
- Voorbeelden van regressieformule met Excel-sjabloon
- Wat is de relatieve standaardafwijkingsformule?
- Hoe correlatie berekenen?