
Inleiding tot de hashfunctie in C
Dit artikel bevat een korte opmerking over hashing (hashtabel en hashfunctie). Het belangrijkste concept is 'zoeken' dat tijdcomplexiteit bepaalt. Om de tijdcomplexiteit te verminderen, wordt elk ander datastructuurconcept geïntroduceerd dat in het gemiddelde geval O (1) tijd heeft en in het slechtste geval O (n) tijd.
Hashing is een techniek met snellere toegang tot elementen die de gegeven gegevens in kaart brengt met een mindere sleutel voor vergelijkingen. Over het algemeen worden bij deze techniek de toetsen met behulp van de hash-functie getraceerd in een tabel die de hash-tabel wordt genoemd.
Wat is de hashfunctie?
De hashfunctie is een functie die de constante-tijdbewerking gebruikt om de waarde uit de hashtabel op te slaan en op te halen, die op de toetsen wordt toegepast als gehele getallen en dit wordt gebruikt als het adres voor waarden in de hashtabel.
Soorten hashfuncties
De soorten hash-functies worden hieronder uitgelegd:
1. Divisiemethode
Bij deze methode is de hash-functie afhankelijk van de rest van een deling.
Voorbeeld: elementen die in een hashtabel moeten worden geplaatst, zijn 42, 78, 89, 64 en laten we de tafelgrootte als 10 nemen.
Hash (sleutel) = Elementen% tabelgrootte;
2 = 42% 10;
8 = 78% 10;
9 = 89% 10;
4 = 64% 10;
De tabelweergave kan als volgt worden gezien:
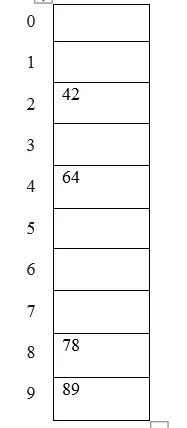
2. Middenvierkant methode
Bij deze methode wordt het middelste deel van het vierkante element als index genomen.
Element dat in de hashtabel moet worden geplaatst, is 210, 350, 99, 890 en de grootte van de tafel is 100.
210 * 210 = 44100, index = 1 omdat het middelste deel van het resultaat (44100) 1 is.
350 * 350 = 122500, index = 25 omdat het middelste deel van het resultaat (122500) 25 is.
99 * 99 = 9801, index = 80 omdat het middelste deel van het resultaat (9801) 80 is.
890 * 890 = 792100, index = 21 omdat het middelste deel van het resultaat (792100) 21 is.
3. Cijfervouwmethode
In deze methode is het element dat in de tabel uh moet worden geplaatst de hash-toets zingen, die wordt verkregen door de elementen in verschillende delen te verdelen en vervolgens de delen te combineren door enkele eenvoudige wiskundige bewerkingen uit te voeren.
Het te plaatsen element is 23576623, 34687734.
- hash (sleutel) = 235 + 766 + 23 = 1024
- hash-toets) = 34 + 68 + 77 + 34 = 213
Stel dat we bij dit soort hashen getallen hebben van 1- 100 en de grootte van de hashtabel = 10. Elementen = 23, 12, 32
Hash (sleutel) = 23% 10 = 3;
Hash (sleutel) = 12% 10 = 2;
Hash (sleutel) = 32% 10 = 2;
Merk uit het bovenstaande voorbeeld op dat beide elementen 12 en 32 naar de 2e plaats in de tabel wijzen, waar het niet mogelijk is om beide op dezelfde plaats te schrijven, een dergelijk probleem staat bekend als een botsing. Om dit soort problemen te voorkomen, zijn er enkele technieken van hashfuncties die kunnen worden gebruikt.
Soorten botsingstechnieken
Laten we de soorten technieken voor het oplossen van botsingen bespreken:
1. Kettingen
In deze methode, zoals de naam al doet vermoeden, biedt het een reeks dozen voor het record in de tabel met twee elementen. Dus wanneer dergelijke botsingen optreden, fungeren de vakken als een gekoppelde lijst.
Voorbeeld: 23, 12, 32 met tabelgrootte 10.
Hash (sleutel) = 23% 10 = 3;
Hash (sleutel) = 12% 10 = 2;
Hash (sleutel) = 32% 10 = 2;
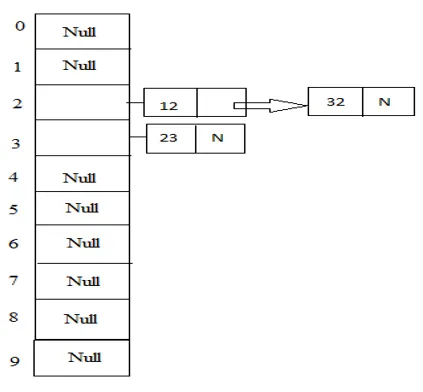
2. Open Adressering
- Lineair onderzoek
Dit is een andere methode om botsingsproblemen op te lossen. Zoals de naam zegt, wanneer er een botsing optreedt, moeten twee elementen op hetzelfde item in de tabel worden geplaatst, maar met deze methode kunnen we zoeken naar de volgende lege ruimte of item in de tabel en het tweede element plaatsen. Dit kan weer tot een ander probleem leiden; als we geen lege invoer in de tabel vinden, leidt dit tot clustering. Dit staat dus bekend als een clusterprobleem dat met de volgende methode kan worden opgelost.
Voorbeeld: 23, 12, 32 met tabelgrootte 10
Hash (sleutel) = 23% 10 = 3;
Hash (sleutel) = 12% 10 = 2;
Hash (sleutel) = 32% 10 = 2;

In dit diagram kunnen 12 en 32 in dezelfde invoer met index 2 worden geplaatst, maar volgens deze methode worden ze lineair geplaatst.
- Kwadratische sondering
Deze methode is een oplossing voor het clusterprobleem tijdens lineair sonderen. In deze methode wordt de hash-functie met hash-toets berekend als hash (toets) = (hash (toets) + x * x)% grootte van de tabel (waarbij x = 0, 1, 2 …).
Voorbeeld: 23, 12, 32 met tabelgrootte 10
Hash (sleutel) = 23% 10 = 3;
Hash (sleutel) = 12% 10 = 2;
Hash (sleutel) = 32% 10 = 2;

Hierin kunnen we zien dat 23 en 12 gemakkelijk kunnen worden geplaatst, maar 32 kan niet opnieuw 12 en 32 delen dezelfde invoer met dezelfde index in de tabel, volgens deze methode hash (key) = (32 + 1 * 1) % 10 = 3. Maar in dit geval wordt tabelinvoer met index 3 geplaatst met 23, dus moeten we x waarde met 1 verhogen. Hash (sleutel) = (32 + 2 * 2)% 10 = 6. Dus we kunnen nu plaatsen 32 in de invoer met index 6 in de tabel.
- Dubbel hashen
Met deze methode moeten we 2 hashfuncties berekenen om het botsingsprobleem op te lossen. De eerste wordt berekend met behulp van een eenvoudige delingsmethode. Ten tweede moet aan twee regels worden voldaan; deze mag niet gelijk zijn aan 0 en vermeldingen moeten worden gesondeerd.
- 1 (sleutel) = sleutel% grootte van de tabel.
- 2 (sleutel) = p - (sleutel mod p), waarbij p priemgetallen <grootte van de tabel is.
Voorbeeld: 23, 12, 32 met tabelgrootte 10
Hash (sleutel) = 23% 10 = 3;
Hash (sleutel) = 12% 10 = 2;
Hash (sleutel) = 32% 10 = 2;
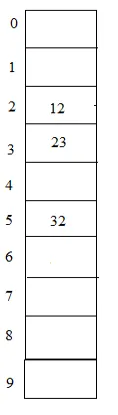
Hierin kan het element 32 opnieuw worden geplaatst met behulp van hash2 (sleutel) = 5 - (32% 5) = 3. Dus 32 kan worden geplaatst op index 5 in de tabel die leeg is omdat we 3 ingangen moeten springen om het te plaatsen.
Conclusie-Hashing-functie in C
Hashing is een van de belangrijke technieken voor het zoeken naar gegevens die zijn voorzien van zeer efficiënte en snelle methoden met behulp van de hashfunctie en hashtabellen. Elk element kan worden gezocht en geplaatst met behulp van verschillende hash-methoden. Deze techniek is qua tijdcoëfficiënt zeer sneller dan welke andere gegevensstructuur ook.
Aanbevolen artikelen
Dit is een gids voor de hashfunctie in C. Hier bespreken we de introductie van de hashfunctie in C, wat is de hashfunctie, soorten hashfuncties, enz. U kunt ook onze andere voorgestelde artikelen bekijken voor meer informatie–
- Hashing in DBMS
- Versleutelingsproces
- Hoe CakePHP te installeren?
- Hoe Blockchain werkt
- Hashing-functie in Java
- Hashing-functie in PHP | Hoe te werken?