
Inleiding tot DFS-algoritme
DFS staat bekend als het diepte-eerste zoekalgoritme dat de stappen biedt om elk knooppunt van een grafiek te doorlopen zonder een knooppunt te herhalen. Dit algoritme is hetzelfde als Depth First Traversal voor een boom, maar verschilt in het onderhouden van een Boolean om te controleren of het knooppunt al is bezocht of niet. Dit is belangrijk voor het doorlopen van de grafiek omdat er ook cycli in de grafiek voorkomen. In dit algoritme wordt een stapel bijgehouden om de zwevende knooppunten op te slaan tijdens het verplaatsen. Het wordt zo genoemd omdat we eerst naar de diepte van elke aangrenzende knoop reizen en dan doorgaan met het doorkruisen van een andere aangrenzende knoop.
Leg het DFS-algoritme uit
Dit algoritme is in tegenstelling tot het BFS-algoritme waarbij alle aangrenzende knooppunten worden bezocht, gevolgd door buren van de aangrenzende knooppunten. Het begint de grafiek vanaf één knooppunt te verkennen en verkent de diepte voordat het terugkeert. Twee dingen worden in dit algoritme overwogen:
- Een hoekpunt bezoeken: selectie van een hoekpunt of knooppunt van de te verplaatsen grafiek.
- Verkenning van een hoekpunt: alle knopen naast dat hoekpunt doorkruisen.
Pseudo-code voor diepte eerste zoekopdracht :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
Lineaire Traversal bestaat ook voor DFS die op 3 manieren kan worden geïmplementeerd:
- Voorafgaande bestelling
- In volgorde
- Postbestelling
Omgekeerde nabestelling is een zeer nuttige manier om te doorlopen en gebruikt bij topologische sortering en verschillende analyses. Er wordt ook een stapel bijgehouden om de knooppunten op te slaan waarvan de verkenning nog in behandeling is.
Grafiekverplaatsing in DFS
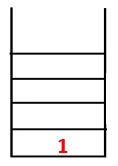
In DFS worden de onderstaande stappen gevolgd om de grafiek te doorlopen. Laten we bijvoorbeeld een gegeven grafiek beginnen met traversal vanaf 1:
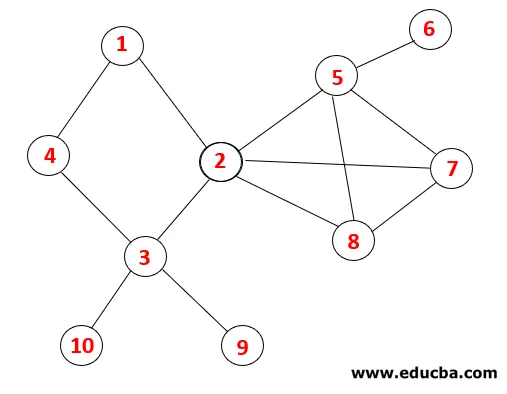
| stack | Doorloopvolgorde | Spanning Tree |
| 1 |  |
|
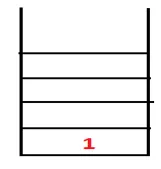 | 1, 4 |  |
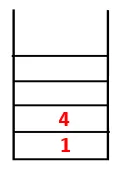 | 1, 4, 3 |  |
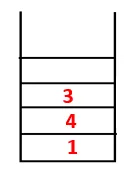 | 1, 4, 3, 10 | 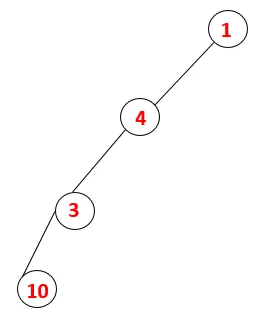 |
 | 1, 4, 3, 10, 9 | 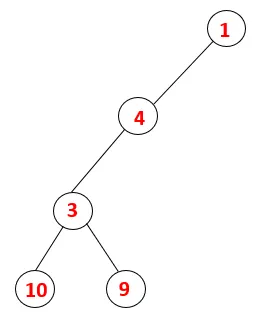 |
 | 1, 4, 3, 10, 9, 2 | 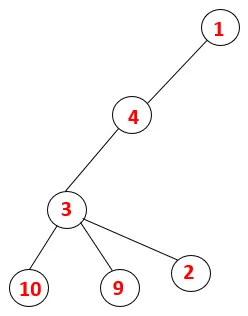 |
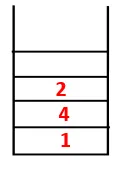 | 1, 4, 3, 10, 9, 2, 8 |  |
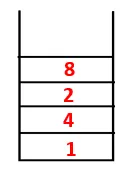 | 1, 4, 3, 10, 9, 2, 8, 7 | 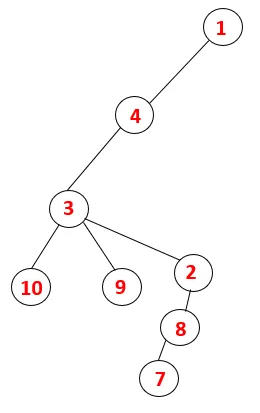 |
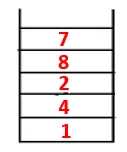 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
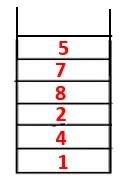 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 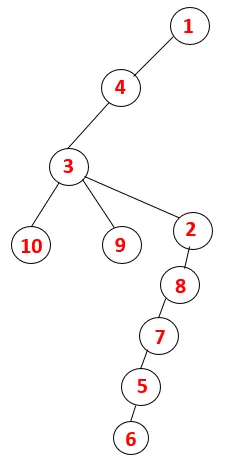 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 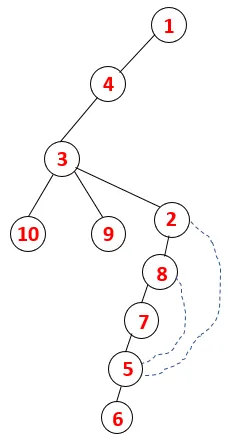 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
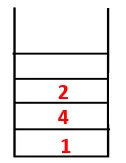 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 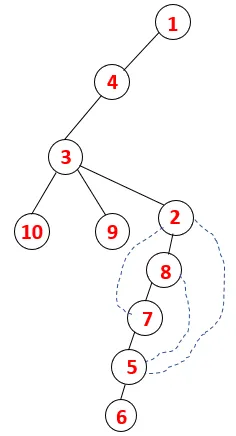 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 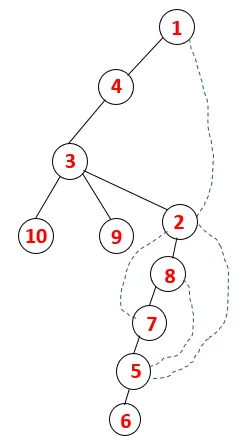 |
Verklaring van het DFS-algoritme
Hieronder staan de stappen naar DFS-algoritme met voor- en nadelen:
Stap 1: Knooppunt 1 wordt bezocht en toegevoegd aan de reeks en de omspannende structuur.
Stap 2: Aangrenzende knooppunten van 1 worden onderzocht, wat 4 is, dus 1 wordt geduwd om te stapelen en 4 wordt in de reeks geduwd en overspant de boom.
Stap 3: Een van de aangrenzende knooppunten van 4 wordt verkend en dus wordt 4 naar de stapel geduwd, en 3 komt in de reeks en overspant boom.
Stap 4: Aangrenzende knooppunten van 3 worden onderzocht door deze op de stapel te drukken en 10 komt in de reeks. Omdat er geen aangrenzende knoop is tot 10, wordt 3 dus uit de stapel geworpen.
Stap 5: Een andere aangrenzende knoop van 3 wordt verkend en 3 wordt op de stapel geduwd en 9 wordt bezocht. Geen aangrenzende knoop van 9 dus 3 wordt eruit gehaald en de laatste aangrenzende knoop van 3 dwz 2 wordt bezocht.
Hetzelfde proces wordt gevolgd voor alle knooppunten totdat de stapel leeg raakt, wat de stopconditie voor het traversale algoritme aangeeft. - -> stippellijnen in de overspannende boom verwijzen naar de achterranden in de grafiek.
Op deze manier worden alle knooppunten in de grafiek doorlopen zonder een van de knooppunten te herhalen.
Voor-en nadelen
- Voordelen: deze geheugenvereisten voor dit algoritme zijn erg minder. Minder ruimte- en tijdcomplexiteit dan BFS.
- Nadelen: oplossing is niet gegarandeerd Toepassingen. Topologische sortering. Bruggen van grafiek vinden.
Voorbeeld om DFS-algoritme te implementeren
Hieronder is het voorbeeld om DFS-algoritme te implementeren:
Code:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Output:
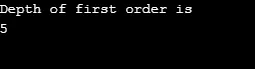
Verklaring van het bovenstaande programma: We hebben een grafiek gemaakt met 5 hoekpunten (0, 1, 2, 3, 4) en hebben de bezochte array gebruikt om alle bezochte hoekpunten bij te houden. Vervolgens herhaalt zich voor elk knooppunt waarvan de aangrenzende knooppunten bestaan, hetzelfde algoritme totdat alle knooppunten zijn bezocht. Vervolgens gaat het algoritme terug naar het aanroepen van hoekpunt en springt het uit de stapel.
Conclusie
De geheugenvereiste van deze grafiek is minder in vergelijking met BFS omdat slechts één stapel nodig is om te worden onderhouden. Een DFS die boom- en traversale reeks omspant, wordt als resultaat gegenereerd maar is niet constant. Meerdere doorloopvolgorde is mogelijk, afhankelijk van het gekozen startpunt en het gekozen verkenningspunt.
Aanbevolen artikelen
Dit is een gids voor DFS-algoritme. Hier bespreken we stap voor stap uitleg, doorkruisen de grafiek in een tabelformaat met voor- en nadelen. U kunt ook onze andere gerelateerde artikelen doornemen voor meer informatie -
- Wat is HDFS?
- Diepgaande leeralgoritmen
- HDFS-opdrachten
- SHA-algoritme