Inleiding tot hiërarchische clustering
- Onlangs vroeg een van onze klanten ons team om een lijst met segmenten uit te brengen met een volgorde van belangrijkheid bij hun klanten om hen te targeten op een van hun nieuw gelanceerde producten. Het is duidelijk dat alleen het segmenteren van de klanten met behulp van gedeeltelijke clustering (k-gemiddelden, c-fuzzy) niet de volgorde van belangrijkheid naar voren brengt, waar hiërarchische clustering in beeld komt.
- Hiërarchische clustering is het scheiden van de gegevens in verschillende groepen op basis van enkele overeenkomsten die bekend staan als clusters, die in wezen gericht zijn op het bouwen van de hiërarchie tussen clusters. Het is in principe onbewaakt leren en het kiezen van de attributen om de gelijkenis te meten is applicatiespecifiek.
The Cluster of Data Hierarchy
- Agglomeratieve clustering
- Divisive Clustering
Laten we een voorbeeld nemen van gegevens, cijfers verkregen door 5 studenten om ze te groeperen voor een aankomende competitie.
| Leerling | Marks |
| EEN | 10 |
| B | 7 |
| C | 28 |
| D | 20 |
| E | 35s |
1. Agglomeratieve clustering
- Om te beginnen beschouwen we elk afzonderlijk punt / element hier als clusters en blijven we de vergelijkbare punten / elementen samenvoegen om een nieuwe cluster op het nieuwe niveau te vormen totdat we achterblijven bij de enkele cluster is een bottom-up benadering.
- Enkele koppeling en volledige koppeling zijn twee populaire voorbeelden van agglomeratieve clustering. Anders dan dat Gemiddelde koppeling en Centroid-koppeling. In een enkele koppeling voegen we in elke stap de twee clusters samen, waarvan de twee dichtstbijzijnde leden de kleinste afstand hebben. In volledige koppeling voegen we de leden van de kleinste afstand samen die de kleinste maximale paarsgewijze afstand bieden.
- Nabijheidsmatrix, het is de kern voor het uitvoeren van hiërarchische clustering, die de afstand tussen elk van de punten geeft.
- Laten we een naderingsmatrix maken voor onze gegevens in de tabel, omdat we de afstand tussen elk van de punten met andere punten berekenen, het zal een asymmetrische matrix met vorm n × n zijn, in ons geval 5 × 5 matrices.
Een populaire methode voor afstandsberekeningen zijn:
- Euclidische afstand (kwadraat)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Manhattan afstand
dist((x, y), (a, b)) =|x−c|+|y−d|
Euclidische afstand wordt het meest gebruikt, we zullen hier hetzelfde gebruiken en we zullen met complexe koppeling gaan.
| Student (Clusters) | EEN | B | C | D | E |
| EEN | 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 | 21 | 13 | 28 |
| C | 18 | 21 | 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 | 15 |
| E | 25 | 28 | 7 | 15 | 0 |
Diagonale elementen van de benaderingsmatrix zullen altijd 0 zijn, omdat de afstand tussen het punt met hetzelfde punt altijd 0 zal zijn, dus diagonale elementen zijn uitgesloten van overweging voor groepering.
Hier, in iteratie 1, is de kleinste afstand 3, dus voegen we A en B samen om een cluster te vormen, opnieuw vormen we een nieuwe naderingsmatrix met cluster (A, B) door (A, B) clusterpunt als 10 te nemen, dwz maximaal van ( 7, 10) zo zou de nieuw gevormde naderingsmatrix zijn
| clusters | (A, B) | C | D | E |
| (A, B) | 0 | 18 | 10 | 25 |
| C | 18 | 0 | 8 | 7 |
| D | 10 | 8 | 0 | 15 |
| E | 25 | 7 | 15 | 0 |
In iteratie 2, 7 is de minimale afstand, dus we voegen C en E samen en vormen een nieuwe cluster (C, E), we herhalen het proces dat wordt gevolgd in iteratie 1 tot we eindigen met de enkele cluster, hier stoppen we bij iteratie 4.
Het hele proces wordt weergegeven in de onderstaande afbeelding:
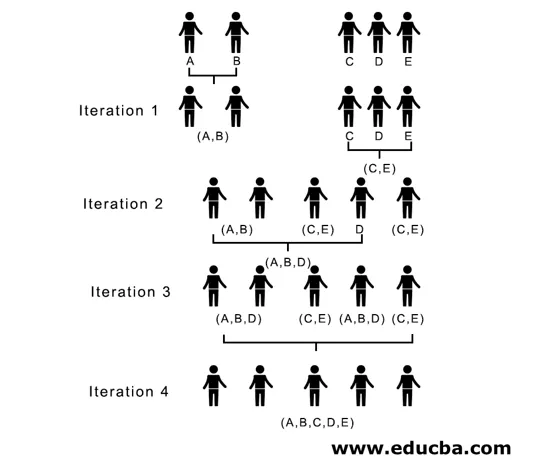
(A, B, D) en (D, E) zijn de 2 clusters gevormd bij iteratie 3, bij de laatste iteratie kunnen we zien dat we nog een enkele cluster hebben.
2. Divisive Clustering
Om te beginnen beschouwen we alle punten als een enkele cluster en scheiden ze op de verste afstand tot we eindigen met individuele punten als individuele clusters (niet noodzakelijkerwijs kunnen we halverwege stoppen, hangt af van het minimum aantal elementen dat we in elke cluster willen) bij elke stap. Het is precies het tegenovergestelde van agglomeratieve clustering en het is een top-downbenadering. Divisive clustering is een manier waarop repetitieve k clustering betekent.
Kiezen tussen Agglomerative en Divisive Clustering is weer afhankelijk van de toepassing, maar er zijn weinig punten waarmee rekening moet worden gehouden:
- Divisive is complexer dan agglomeratieve clustering.
- Deels clustering is efficiënter als we geen volledige hiërarchie tot op individuele gegevenspunten genereren.
- Agglomeratieve clustering neemt een beslissing door rekening te houden met de lokale patronen, zonder in eerste instantie rekening te houden met globale patronen die niet kunnen worden teruggedraaid.
Visualisatie van hiërarchische clustering
Een super handige methode om hiërarchische clustering te visualiseren die in het bedrijfsleven helpt, is Dendogram. Dendogrammen zijn boomachtige structuren die de opeenvolging van samenvoegingen en splitsingen registreren waarin verticale lijn de afstand tussen de clusters voorstelt, de afstand tussen verticale lijnen en de afstand tussen de clusters is recht evenredig, dat wil zeggen hoe meer afstand de clusters waarschijnlijk ongelijk zijn.
We kunnen het dendogram gebruiken om het aantal clusters te bepalen, teken gewoon een lijn die snijdt met een langste verticale lijn op het dendogram, een aantal verticale lijnen wordt het aantal te beschouwen clusters.
Hieronder is het voorbeeld Dendogram.
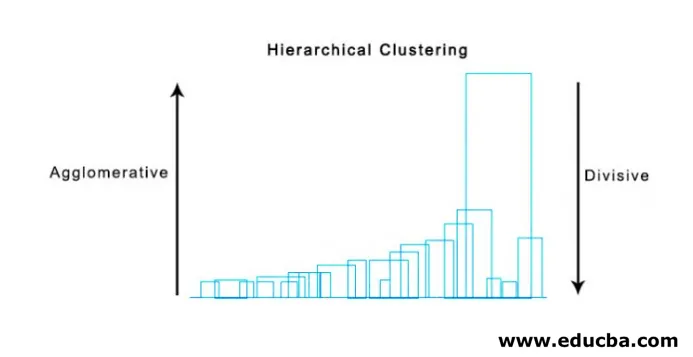
Er zijn vrij eenvoudige en directe python-pakketten en zijn functies om hiërarchische clustering en plotdendogrammen uit te voeren.
- De hiërarchie van Scipy.
- Cluster.hierarchy.dendogram voor visualisatie.
Algemene scenario's waarin hiërarchische clustering wordt gebruikt
- Klantsegmentatie naar product- of servicemarketing.
- Stadsplanning om de plaatsen te identificeren om structuren / diensten / gebouwen te bouwen.
- Sociale netwerkanalyse identificeert bijvoorbeeld alle MS Dhoni-fans om reclame te maken voor zijn biopic.
Voordelen van hiërarchische clustering
De voordelen worden hieronder gegeven:
- In het geval van gedeeltelijke clustering zoals k-middelen moet het aantal clusters bekend zijn voorafgaand aan clustering, wat niet mogelijk is in praktische toepassingen, terwijl in hiërarchische clustering geen voorkennis van het aantal clusters vereist is.
- Hiërarchische clustering levert een hiërarchie op, dat wil zeggen een structuur die informatiever is dan de ongestructureerde set van de platte clusters die worden geretourneerd door gedeeltelijke clustering.
- Hiërarchische clustering is eenvoudig te implementeren.
- Brengt resultaten naar voren in de meeste scenario's.
Conclusie
Type clustering maakt het grote verschil wanneer gegevens worden gepresenteerd, waarbij hiërarchische clustering informatiever en eenvoudiger te analyseren is heeft de voorkeur boven gedeeltelijke clustering. En het wordt vaak geassocieerd met warmtekaarten. Niet te vergeten attributen die worden gekozen om de gelijkenis of ongelijkheid te berekenen, hebben voornamelijk invloed op zowel clusters als hiërarchie.
Aanbevolen artikelen
Dit is een handleiding voor hiërarchische clustering. Hier bespreken we de introductie, voordelen van hiërarchische clustering en gemeenschappelijke scenario's waarin hiërarchische clustering wordt gebruikt. U kunt ook onze andere voorgestelde artikelen doornemen voor meer informatie–
- Clustering Algoritme
- Clustering in machine learning
- Hiërarchische clustering in R
- Clustering methoden
- Hoe de hiërarchie in Tableau verwijderen?