
Samengestelde jaarlijkse groeisnelheidformule (inhoudsopgave)
- Formule
- Voorbeelden
- Rekenmachine
Wat is de samengestelde jaarlijkse groeisnelheidformule?
Compounding is het effect waarbij een investering niet alleen rente op de hoofdcomponent verdient, maar ook rente op rente oplevert. Dus samengestelde jaarlijkse groeisnelheid is de effectieve jaarlijkse groei die wordt verdiend met investeringen, rekening houdend met het in beeld brengen. Dit veronderstelt in feite dat de jaarlijks verdiende rente wordt herbelegd en dezelfde rente verdient als de hoofdsom. Dat is de reden dat de samengestelde jaarlijkse groeivoet altijd hoger is dan de eenvoudige rentevoet. Veel beleggingen zoals beleggingsfondsen, beursrendement zijn niet erg lineair en op een zeer onstabiele manier.
Samengestelde jaarlijkse groeivoet helpt bij het gladmaken van dat rendement en zal uitwijzen hoeveel een belegger tijdens de looptijd van de investering heeft verdiend, gezien het feit dat alle inkomsten tussen die periode tegen dezelfde koers worden herbelegd. Vanwege dit gladmakende effect helpt het ons bij het vergelijken van datasets met verschillende niveaus van volatiliteit. Het wordt zeer vaak gebruikt voor financiële analyse.
Einde investeringsbedrag = Startbedrag (1 + CAGR) Aantal jaren
De formule voor samengestelde jaarlijkse groeisnelheid -
CAGR = (Ending Investment Amount / Start Amount) (1 / Number of Years) – 1
Deze formule is van toepassing als de investering jaarlijks wordt verergerd, wat betekent dat we het geld op jaarbasis herinvesteren. Maar soms gebeurt het dat we de snelheid willen berekenen waarin de samenstelling plaatsvindt op kwartaalbasis, maandelijks, dagelijks. Daarom gebruiken we de onderstaande formule:
Einde investeringsbedrag = startbedrag (1 + CAGR / samengestelde frequentie) (aantal jaren * samengestelde frequentie)
Dus een formule voor samengestelde jaarlijkse groeisnelheid -
CAGR = Compounding Frequency * ((Ending Investment Amount / Start Amount) (1 / (Number of Years * Compounding Frequency)) – 1)
Samengestelde frequentie:
- Halfjaarlijkse samenstelling: 2
- Kwartaalsamenstelling: 4
- Maandelijkse frequentie: 12 enzovoort
Voorbeelden van CAGR-formule (met Excel-sjabloon)
Laten we een voorbeeld nemen om de berekening van de CAGR-formule beter te begrijpen.
U kunt deze samengestelde jaarlijkse groeisnelheid Excel-sjabloon hier downloaden - Samengestelde jaarlijkse groeisnelheid Excel-sjabloonCAGR-formule - Voorbeeld # 1
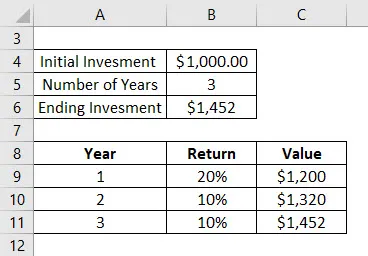
Stel dat u drie jaar geleden $ 1000 in beleggingsfondsen heeft geïnvesteerd. Hierna volgt het rendement dat u voor deze 3 jaar hebt gekregen:
- 1 e jaar, heb je een waardestijging van 20%. Dus de totale waarde is $ 1200 aan het einde van het eerste jaar
- 2e jaar, kreeg u een waardetoename van 10%. Dus de totale waarde is $ 1320 aan het einde van het tweede jaar
- 3e jaar, kreeg u een waardetoename van 10%. Dus de totale waarde is $ 1452 aan het einde van het derde jaar
CAGR wordt berekend met behulp van de onderstaande formule
CAGR = (Beëindigend investeringsbedrag / startbedrag) (1 / aantal jaren) - 1
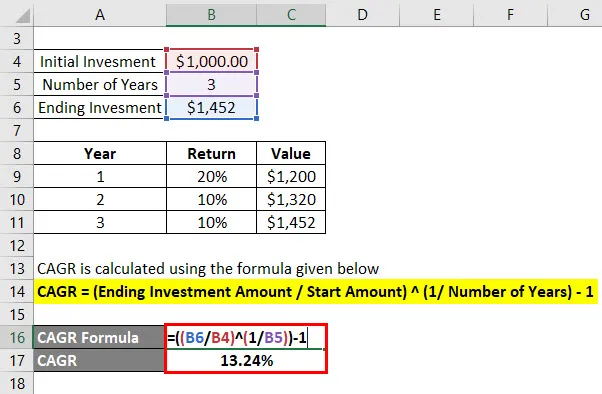
- CAGR = ($ 1, 452 / $ 1.000) (1/3) - 1
- CAGR = 13, 24%
Hier kunnen we zien dat het jaarrendement voor alle 3 jaar anders is en varieert, maar de samengestelde jaarlijkse groeisnelheid geeft ons een enkele rente die we kunnen vergelijken met verschillende investeringsmogelijkheden.
CAGR-formule - Voorbeeld # 2
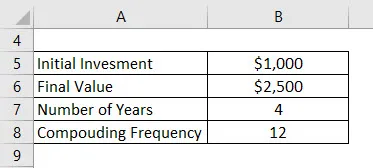
Stel dat u $ 1000 in de bank heeft geïnvesteerd en dat u het geld 4 jaar op de bank wilt houden. Laten we nu zeggen dat het totale bedrag dat u na 4 jaar krijgt $ 2500 is. Een bank biedt een tarief met maandelijkse samenstelling. Bereken CAGR.
CAGR wordt berekend met behulp van de onderstaande formule
CAGR = samengestelde frequentie * ((einde investeringsbedrag / startbedrag) (1 / (aantal jaren * samengestelde frequentie)) - 1)
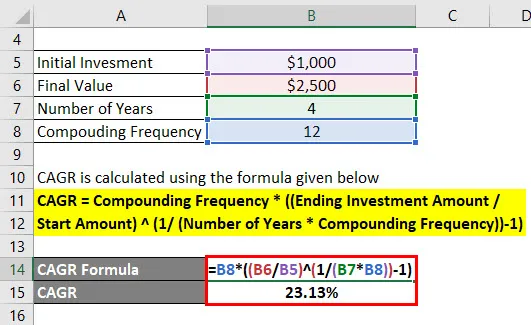
- CAGR = 12 * (($ 2500 / $ 1.000) (1 / (4 * 12)) - 1)
- CAGR = 23, 13%
Het samengestelde jaarlijkse groeipercentage is dus 23, 13%.
Verklaring van de samengestelde jaarlijkse groeivoetformule
Hoewel het samengestelde jaarlijkse groeipercentage het jaarlijkse tarief voor de investering is, is dit slechts een theoretisch cijfer en is dit niet het werkelijke rendement. De belangrijkste veronderstelling hierbij is dat alle inkomsten worden herbelegd tegen dezelfde koers voor de investeringsperiode, maar de koers blijft niet voor alle jaren en we beleggen ons geld mogelijk niet tegen dezelfde koers. Het is dus een enige representatieve koers die ons vertelt dat we zouden kunnen eindigen als al het geld aan het einde van elk jaar met die koers wordt herbelegd. Er zijn dus enkele kernpunten waarmee we rekening moeten houden bij het gebruik van een samengestelde jaarlijkse groeivoet.
We zullen ook heel voorzichtig zijn met een investering die lang duurt. Als een beleggingsperiode bijvoorbeeld erg lang is, bijvoorbeeld 20 jaar, kan de samengestelde jaarlijkse rente ons de verkeerde indicatie geven, omdat het kan gebeuren dat we de eerste 15 jaar geen winst maken en alle rendementen in de afgelopen periode komen . 15 jaar lang geen winst maken is voor geen enkel bedrijf acceptabel.
Evenzo, als twee investeringsmogelijkheden dezelfde CAGR hebben, kan het zijn dat de ene meer aangetrokken is dan de andere vanwege de reden dat groei in de ene plaatsvindt in de beginperiode, terwijl de andere zich concentreert aan het einde van de periode.
Relevantie en gebruik van de samengestelde jaarlijkse groeivoetformule
Het samengestelde jaarlijkse groeipercentage is echt nuttig bij het berekenen van het gemiddelde groeipercentage van de investering en kan helpen bij het vergelijken van verschillende investeringen. Zoals we in het bovenstaande voorbeeld hebben gezien, is de groei van de investeringen van jaar tot jaar ongelijk en onregelmatig. Maar met behulp van samengestelde jaarlijkse groei, vloeit het rendement af. Een andere factor die een samengesteld jaarlijks groeipercentage tot een kritische methode maakt bij het bepalen van de groei van een investering, is dat het rekening houdt met het samengestelde effect, welk jaarlijks rendement dat niet doet. Samengestelde jaarlijkse rente geeft ons niet het werkelijke beeld van het rendement, omdat het alleen het rendement op de hoofdsom berekent en de rente op de rentecomponent negeert, maar dit is niet het geval met de samengestelde jaarlijkse groeivoet.
Samengestelde jaarlijkse groeicijferformule-calculator
U kunt de volgende samengestelde jaarlijkse groeipercentagescalculator gebruiken
| Investeringsbedrag beëindigen | |
| Startbedrag | |
| Aantal jaren | |
| CAGR | |
| CAGR = | ((Einde investeringsbedrag / startbedrag) 1 / Aantal jaren -1) |
| = | ((0/0) 1/0 -1) = 0 |
Aanbevolen artikelen
Dit is een leidraad geweest voor de formule van de samengestelde jaarlijkse groeivoet. Hier bespreken we hoe CAGR te berekenen, samen met praktische voorbeelden. We bieden ook een samengestelde jaarlijkse groeicalculator met een downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Gids voor tarief van terugkeerformule
- Voorbeelden van exponentiële groeiformule
- Calculator voor centrale limietstelling formule
- Hoe marktkapitalisatie berekenen?