Inleiding tot hiërarchisch clusteringalgoritme
Het hiërarchische clusteringalgoritme is een techniek zonder machinaal leren. Het is gericht op het vinden van natuurlijke groepen op basis van de kenmerken van de gegevens.
Het hiërarchische cluster-algoritme is bedoeld om geneste groepen van gegevens te vinden door de hiërarchie te bouwen. Het is vergelijkbaar met de biologische taxonomie van het planten- of dierenrijk. Hiërarchische clusters worden over het algemeen weergegeven met behulp van de hiërarchische structuur die bekend staat als een dendrogram.
Soorten hiërarchisch clusteringalgoritme
Hiërarchische clusteringalgoritmen zijn van 2 soorten:
- Divisive
- agglomeratief
1. Deels
Dit is een top-downbenadering, waarbij eerst de volledige gegevens als één groep worden beschouwd en vervolgens de gegevens iteratief in subgroepen worden opgesplitst. Als het nummer van een hiërarchisch clusteringalgoritme bekend is, stopt het proces van delen zodra het aantal clusters is bereikt. Anders stopt het proces wanneer de gegevens niet meer kunnen worden gesplitst, wat betekent dat de subgroep die is verkregen uit de huidige iteratie dezelfde is als die uit de vorige iteratie (men kan ook overwegen dat de verdeling stopt wanneer elk gegevenspunt een cluster is ).
2. Agglomeratief
Het is een bottom-up benadering die steunt op het samenvoegen van clusters. Aanvankelijk worden de gegevens opgesplitst in m singleton-clusters (waarbij de waarde van m het aantal monsters / gegevenspunten is). Twee clusters worden iteratief samengevoegd, waardoor het aantal clusters bij elke iteratie wordt verminderd. Dit proces van samenvoegen van clusters stopt wanneer alle clusters zijn samengevoegd tot één of het aantal gewenste clusters is bereikt.
Op niveau 1 zijn er m clusters die worden gereduceerd tot 1 cluster op niveau m. De gegevenspunten die worden samengevoegd om een cluster op een lager niveau te vormen, blijven ook op de hogere niveaus in hetzelfde cluster. Stel bijvoorbeeld dat er 8 punten x1..x8 zijn, dus aanvankelijk zijn er 8 clusters op niveau 1. Stel dat de punten x1 en x2 worden samengevoegd in een cluster op niveau 2, dan blijven ze tot niveau 8 in dezelfde cluster.
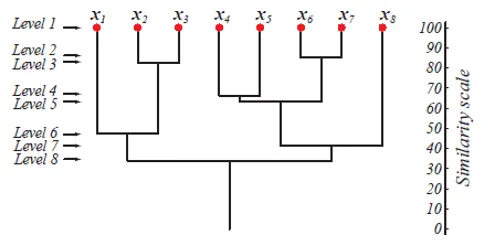
De bovenstaande afbeelding toont een dendrogramrepresentatie van de agglomeratieclusteringbenadering voor 8 datapunten en de overeenkomstenschaal die overeenkomt met elk niveau.
De niveaus van clusters geven ons een idee van hoe vergelijkbaar de gegevenspunten in de clusters zijn. Zoals weergegeven in figuur 1, worden de gegevenspunten eerder samengevoegd tot een cluster, op dezelfde manier als ze zijn. De gegevenspunten binnen een cluster op niveau 2 (bijvoorbeeld x2 en x3) zijn dus meer vergelijkbaar dan die gegevenspunten in een cluster op niveau 6 (bijvoorbeeld x1 en x2).
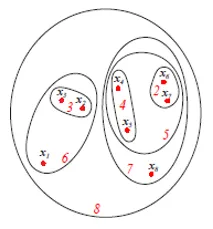
De bovenstaande afbeelding toont de Set of Venn-diagramweergave van de agglomeratieve clusteringbenadering van de bovengenoemde 8 gegevenspunten. Zowel dendrograms als setrepresentaties kunnen worden gebruikt voor clustering. Een dendrogram heeft echter meestal de voorkeur dat activapresentatie de cluster-overeenkomsten niet kwantitatief kan weergeven.
Stappen voor hiërarchisch clusteringalgoritme
Laten we de volgende stappen volgen voor het hiërarchische clusteringalgoritme dat hieronder wordt gegeven:
1. Algoritme
Agglomeratief hiërarchisch clusteringalgoritme
- Begin met initialiseren c, c1 = n, Di = (xi), i = 1, …, n '
- Doe c1 = c1 - 1
- Zoek dichtstbijzijnde clusters, zeg, Di en Dj
- Voeg Di en Dj samen
- Tot c = c1
- Retourneer c-clusters
- Einde
Dit algoritme begint aanvankelijk met n clusters waarbij elk gegevenspunt een cluster is. Bij elke iteratie wordt het aantal clusters met 1 verminderd naarmate de 2 dichtstbijzijnde clusters worden samengevoegd. Dit proces gaat door totdat het aantal clusters wordt gereduceerd tot de vooraf gedefinieerde waarde c.
Hoe te beslissen welke clusters in de buurt zijn?
Dat wordt gedefinieerd met behulp van verschillende afstandsstatistieken die als volgt zijn:
- De minimale afstand tussen de clusters dmin (Di, Dj). Handig voor single.
- De maximale afstand tussen de clusters dmax (Di, Dj). Handig om te voltooien.
- De gemiddelde afstand tussen de clusters davg (Di, Dj).
Wat is een enkele koppeling en volledige koppeling?
- Wanneer dmin (di, dj) wordt gebruikt om de afstand tussen twee clusters te vinden en het algoritme eindigt als de afstand tussen de dichtstbijzijnde clusters een drempel overschrijdt, wordt het algoritme een algoritme voor een enkele koppeling genoemd.
- Wanneer dmax (Di, Dj) wordt gebruikt om de afstand tussen twee clusters te vinden en het algoritme eindigt als de afstand tussen de dichtstbijzijnde clusters een drempel overschrijdt, wordt het algoritme een compleet koppelingsalgoritme genoemd.
- Laten we elk gegevenspunt beschouwen als een knooppunt van een grafiek. Er is een rand tussen twee gegevenspunten als ze tot hetzelfde cluster behoren. Wanneer twee dichtstbijzijnde clusters worden samengevoegd, wordt een rand toegevoegd. Het wordt een enkele koppeling genoemd omdat er een uniek pad bestaat van het ene knooppunt naar het andere.
- Het complete koppelingsalgoritme voegt twee clusters samen door de afstand tussen de twee verste punten te minimaliseren.
- Een enkel koppelingsalgoritme genereert een overspannende boom. Dit algoritme is echter gevoelig voor ruis. Een compleet koppelingsalgoritme genereert een complete grafiek.
Wat is de tijdcomplexiteit van het algoritme?
Stel dat we n patronen in de d-dimensionale ruimte hebben en we gebruiken dmin (Di, Dj) om c-clusters te vormen. We moeten de n-n-1-afstanden tussen punten berekenen - die elk een O (d 2 ) -berekening zijn - en de resultaten in een afstandtabel tussen punten plaatsen. De ruimtecomplexiteit is O (n 2 ). Het vinden van het minimale afstandspaar (voor de eerste samenvoeging) vereist dat we de volledige lijst doorlopen, met behoud van de index van de kleinste afstand.
Dus voor de eerste agglomeratieve stap is de complexiteit O (n (n - 1) (d2 + 1)) = O (n 2 d2). Voor een andere willekeurige agglomeratiestap (dwz van c1 tot c1 - 1), stappen we alleen door de n (n - 1) - c1 "ongebruikte" afstanden in de lijst en vinden we de kleinste waarvoor x en x 'in verschillende clusters liggen . Dit is opnieuw O (n (n − 1) −c1). De totale tijdcomplexiteit is dus O (cn 2 d 2 ), en in typische omstandigheden n >> c.
2. Visualisatie
Nadat de gegevens in clusters zijn gesplitst, is het een goede gewoonte om de clusters te visualiseren om een idee te krijgen van hoe de groepering eruit ziet. Maar het visualiseren van deze hoogdimensionale gegevens is moeilijk. Daarom gebruiken we Principal Component Analysis (PCA) voor visualisatie. Na PCA verkrijgen we de gegevenspunten in de laag-dimensionale ruimte (meestal 2D of 3D) die we kunnen plotten om de groepering te zien.
Opmerking: Hoge dimensie betekent een groot aantal functies en niet een aantal gegevenspunten.3. Evaluatie
Een van de methoden voor de evaluatie van clusters is dat de afstand van de punten tussen de clusters (interclusterafstand) veel groter moet zijn dan de afstand van de punten binnen het cluster (intraclusterafstand).
Conclusie
Hier volgen enkele belangrijke afhaalrestaurants:
- Het hiërarchische clusteringalgoritme wordt gebruikt om geneste patronen in gegevens te vinden
- Hiërarchische clustering is van 2 soorten - Divisive en Agglomerative
- Dendrogram en set / Venn-diagram kunnen worden gebruikt voor weergave
- Enkele koppeling voegt twee clusters samen door de minimale afstand ertussen te minimaliseren. Het vormt een spanning
- Volledige koppeling voegt twee clusters samen door de maximale afstand te minimaliseren. Het vormt een complete grafiek.
- De totale tijdcomplexiteit van hiërarchisch clusteringalgoritme is O (cn 2 d 2 ), waarbij c het vooraf gedefinieerde aantal clusters is, n het aantal patronen is en d de d-dimensionale ruimte van de n patronen is.
Aanbevolen artikelen
Dit is een handleiding voor het hiërarchische cluster-algoritme. Hier bespreken we de soorten en stappen van hiërarchische clusteringalgoritmen. U kunt ook de volgende artikelen bekijken voor meer informatie-
- Hiërarchische clusteranalyse
- Hiërarchische clustering in R '
- Clustering Algoritme
- Wat is clustering in datamining?
- Hiërarchische clustering | Agglomerative & Divisive Clustering
- C ++ Algoritme | Voorbeelden van C ++ algoritme