
Inleiding tot de Fibonacci-serie in Python
Fibonacci-serie in Python, dit wordt een reeks getallen genoemd, waarbij het volgende getal de som is van de huidige twee getallen.
Bijvoorbeeld:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ..zo verder
Dus hier 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 enzovoort.
Als we naar het bovenstaande kijken, zou men een bepaald idee hebben gekregen waar we het over hebben.
In termen van wiskundige regels kan het echter worden geschreven als:

Waar nde nummer de som is van het nummer op plaatsen (n-1) en (n-2). Als het gaat om de implementatie van de Fibonacci-serie, kan er een aantal coderingstalen zijn waarmee dit kan worden gedaan.
Python is tegenwoordig echter een veel gebruikte taal. Laten we de implementatie van de Fibonacci-serie bekijken via Python. Men moet zich bewust zijn van basisconditioneringsverklaringen zoals de lus, if-else, while lus, enz. In Python, voordat u hier verder gaat. Zo niet, dan zou het geweldig zijn als men het kan herzien en vervolgens de komende inhoud kan opnemen. Hier voor demo-doeleinden gebruik ik spyder die IDE is voor python programmeertaal. Men kan ook andere IDE- of Ipython-notebooks gebruiken voor de uitvoering van de Python-programma's.
Fibonacci-serie in Python
Laten we eens kijken naar de implementatie van het Fibonacci-nummer en de serie, gezien de eerste twee elementen van Fibonacci zijn 0 en 1:
U kunt echter de functie van Fibonacci aanpassen volgens uw vereiste, maar eerst de basisbeginselen bekijken en geleidelijk overgaan op anderen.
Python-code voor het vinden van het Fibonacci-nummer
Code 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Code 2:
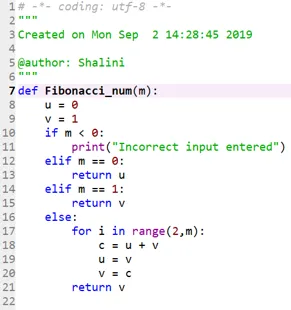
Output:
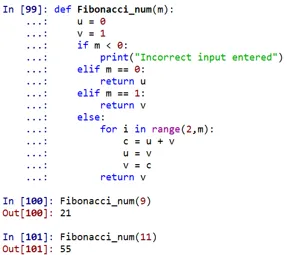
Zoals men kan zien, zou het Fibonacci-getal op de 9e plaats 21 zijn en op de 11e plaats 55.
- Hier is "fibonacci_num" een gedefinieerde functie, die zorgt voor het vinden van het Fibonacci-nummer met behulp van bepaalde voorwaarden. Deze functie kan worden opgeroepen door een willekeurige positie op te geven.
Laten we nu eens kijken hoe men series kan afdrukken tot de genoemde positie:
Code:
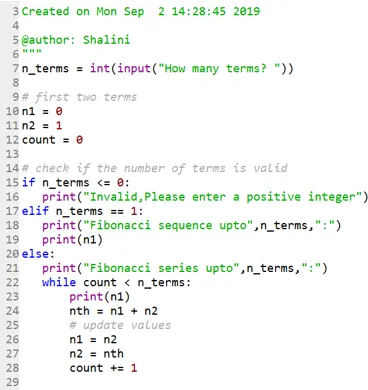
Output:
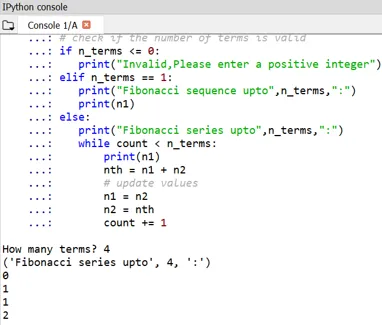
Men ziet dat het begin van Fibonacci-nummers is gedefinieerd als 0 en 1.
- Als iemand zijn eigen starttermen wil definiëren, kan dat ook op dezelfde manier door n1 en n2 aan te passen. Hier is het voorbeeld daarvoor:
Laten we zeggen dat we onze startvoorwaarden willen zijn: n1 = 3, n2 = 5
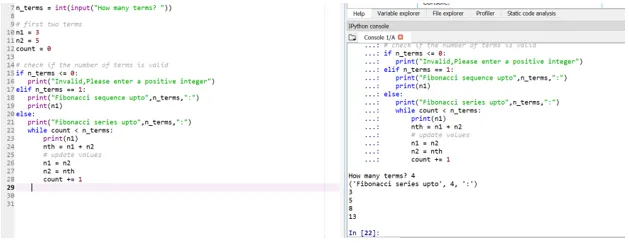
Dus hier wordt uw 4e termijnpositie (gebruikersinvoer wordt ingenomen) bepaald op basis van uw startvoorwaarden.
Methoden waarmee Fibonacci-serie kan worden gegenereerd
Hieronder staan de drie methoden waarmee Fibonacci-serie kan worden gegenereerd:
1. Via generatoren
Code:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Output:
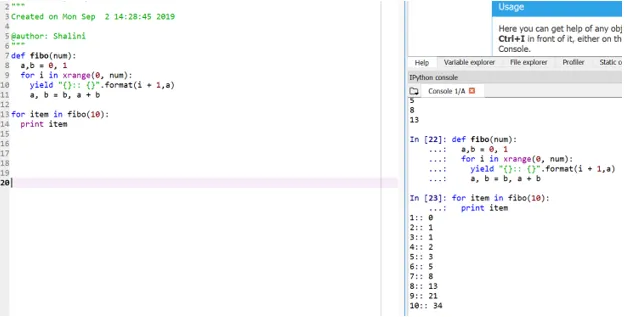
Deze methode wordt "generator" genoemd omdat de functie xrange een generator is van de getallen tussen 0 en num en opbrengst de generator is voor geformatteerde uitvoer.
Dit is wat xrange voor u doet:

Hier is de Fibonacci-serie gedefinieerd in de vorm van een functie, waarbinnen de lus-, xrange- en opbrengstfunctie voor de uitvoer zorgt.
2. Door voor lus
Code:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Output:

Zoals men kan zien, is simple for loop gebruikt om de Fibonacci-serie tussen 0 en 10 af te drukken. Binnen voor loop zijn nieuwe waarden aan de variabelen toegewezen. U en v zijn de standaard beginwaarden van Fibonacci die respectievelijk op 0 en 1 zijn ingesteld.
Wat betreft de loop die wordt uitgevoerd, is de nieuwe u-waarde de oude v-waarde, terwijl de nieuwe v-waarde de som is van oude waarden van u en v. Dit gaat door tot het einde van de bereikwaarden.
3. Door recursie
Code:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Output:
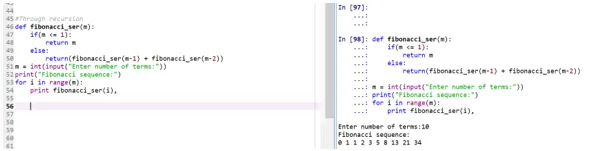
- De functie "fibonacci_ser" roept zichzelf op om de Fibonacci-serie af te drukken.
- En daarom heeft de methode zijn naam "recursie" gekregen.
Stappen die hier zijn gevolgd:
- Hier is de gebruiker gevraagd om de plaats in te voeren tot welke Fibonacci-serie moet worden afgedrukt.
- Nummer gaat door de functie "fibonacci_ser".
- De voorwaarde wordt gecontroleerd, als de opgegeven lengte minder dan 1 is of niet. Zo ja, wordt het resultaat onmiddellijk gegeven.
- Als de lengte echter groter is dan 1, worden recursieve aanroepen gedaan naar "fibonacci_ser" met argumenten met een lengte kleiner dan 1 en 2, namelijk fibonacci_ser (m-1) en fibonacci_ser (m-2).
- Daarom geeft recursie de gewenste uitvoer en drukt u deze af.
- Dus, kort gezegd, hebben we drie manieren besproken om de Fibonacci-serie weer te geven.
- Door voor lus, door generatoren en door recursie.
Alle drie de Python-code samengevat
Hieronder staan de drie python-codes:
1. Via generatoren
Code:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Door voor lus
Code:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Door recursie
Code:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Hierboven zijn alle procedures samengevat, men moet oefenen om een goede grip op iedereen te krijgen.
Output:
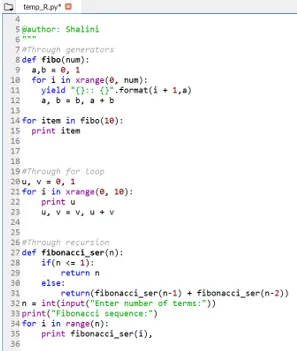
Conclusie
Als je de bovenstaande inhoud van Fibonacci doorneemt, zou je een kristalhelder inzicht hebben gekregen in Fibonacci-nummers en -reeksen, gespecialiseerd in python. Zodra je eenmaal vertrouwd bent met de logica van de Fibonacci-serie, zal het genereren van een andere reeks series, het werken met andere nummers en met verschillende methoden nu een cakewalk voor je zijn. Een logische benadering is de enige manier om hierin uit te blinken.
Aanbevolen artikelen
Dit is een gids voor Fibonacci-serie in Python. Hier bespreken we Fibonacci-getallen en -reeksen, gespecialiseerd in python, het genereren van een andere reeks reeksen, het werken met andere getallen en met verschillende methoden. U kunt ook onze andere gerelateerde artikelen doornemen voor meer informatie -
- Random Number Generator in Python
- Wiskundige functies in Python
- Factorial in Python
- Inkapseling in Python
- Fibonacci-serie in Java
- Python-functies
- Factorieprogramma in JavaScript
- Willekeurige nummergenerator in Matlab
- Willekeurige nummergenerator in C #
- Inkapseling in JavaScript