
Inleiding tot standaardafwijkingsvoorbeelden
Er zijn voldoende voorbeelden van standaardafwijkingen. Standaarddeviatie is de maat voor de spreiding van de gegevensset, dwz hoe gespreid de getallen zijn. Het is handig voor het vergelijken van de verschillende gegevenssets die mogelijk hetzelfde gemiddelde hebben, maar met een ander bereik. Het volgende verschillende voorbeeld van de standaardafwijking geeft inzicht in de meest voorkomende situaties waarin de standaardafwijking wordt berekend en hoe men hetzelfde kan berekenen
Voorbeelden van standaarddeviatie
Hieronder staan de voorbeelden van de standaarddeviatie
Standaardafwijking - Voorbeeld # 1
De voorraad van bedrijf Z verkoopt voor $ 50 per aandeel en dezelfde aanbiedingen voor de volgende uitbetalingen voor het volgende jaar:
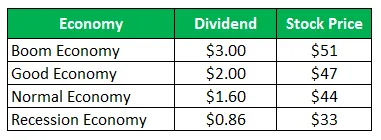
Bereken de standaarddeviatie wanneer alle vier scenario's even waarschijnlijk zijn.
Oplossing:
Berekeningen van Holding Period Return (HPR) zijn als volgt -
Formule van HPR
HPR = ((waarde einde periode - oorspronkelijke waarde) + inkomsten) / oorspronkelijke waarde) * 100
Voor Boom Economy
- HPR (Boom) = ((51-50) + 3) / 50 = 8.00%
- HPR (goed) = ((47-50) + 2) / 50 = -2, 00%
- HPR (Normaal) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (recessie) = ((33-50) + 0, 86) / 50 = -32, 28%
Berekening van verwacht rendement
Omdat alle scenario's even waarschijnlijk zijn, is de waarschijnlijkheid van alle ¼
Formule van verwachte terugkeer
Verwacht rendement = (waarschijnlijkheid van boom * rendement van boom) + (waarschijnlijkheid van goed * rendement van goed) + (waarschijnlijkheid van normaal * rendement van normaal) + (waarschijnlijkheid van recessie * terugkeer van recessie)
- Verwacht rendement = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8.80%) + (1/4 x -32.28%)
- Verwacht rendement = -8.77%
Berekening van standaardafwijking
Formule van variantie
Variantie = (waarschijnlijkheid van giek * (rendement van giek - totaal verwacht rendement) 2) + (waarschijnlijkheid van goed * (rendement van goed - totaal verwacht rendement) 2) + (waarschijnlijkheid van normaal * (rendement van normaal - totaal verwacht rendement) 2 ) + (Kans op recessie * (Terugkeer uit recessie - Totaal verwachte terugkeer) 2)
- Variantie = 1/4 (8 - (-8.77)) 2 + 1/4 (-2 - (-8.77)) 2 + 1/4 (-8.80 - (-8.77)) 2 + 1/4 (-32.28 - (-8.77)) 2
- Variantie = 219, 95
Formule van standaardafwijking
Standaardafwijking is Square Root of Variance
Standaardafwijking = √ Variantie
- Standaardafwijking = √ 219, 95
- Standaardafwijking = 14, 83%
Voorbeeld van standaardafwijking - 2
Standaardafwijking in het geval van twee bedrijven in de portefeuille
De gewone aandelen van bedrijf A verkopen voor $ 28 per aandeel en dezelfde aanbiedingen na uitbetalingen voor het volgende jaar

De gewone aandelen van bedrijf B verkopen voor $ 93 per aandeel en dezelfde aanbiedingen na uitbetalingen voor het volgende jaar:

(a) Bereken de standaardafwijking van bedrijf A
(b) Bereken de standaardafwijking van bedrijf B
(c) Bereken de standaardafwijking van de portefeuille als de helft van de investering wordt gedaan door bedrijf A en de rest door bedrijf B
Oplossing:
Voor bedrijf A
Berekeningen van Hold Period Return (HPR)
Formule van HPR
HPR = ((waarde einde periode - oorspronkelijke waarde) + inkomsten) / oorspronkelijke waarde) * 100
- HPR (boom) = ((20-28) + 1) / 28 = -25.00%
- HPR (Normaal) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (recessie) = ((38-28) + 5) / 28 = 53.57%
Berekening van verwacht rendement van bedrijf A
Formule van verwachte terugkeer
Verwacht rendement = (waarschijnlijkheid van giek * rendement van giek) + (waarschijnlijkheid van normaal * rendement van normaal) + (waarschijnlijkheid van recessie * rendement van recessie)
- Verwacht rendement = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Verwacht rendement = 3, 84%
Berekening van standaarddeviatiebedrijf A
Formule van variantie
Variantie = (Waarschijnlijkheid van giek * (Rendement van giek - Totaal verwacht rendement) 2) + (Waarschijnlijkheid van Normaal * (Rendement van normaal - Totaal verwacht rendement) 2 ) + (Kans op recessie * (Rendement van recessie - Totaal verwacht rendement) 2)
- Variantie = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Variantie = 895.15
Formule van standaardafwijking
Standaardafwijking is Square Root of Variance
Standaardafwijking = √ Variantie
- Standaardafwijking = √ 895.15
- Standaardafwijking = 29, 92%
Voor bedrijf B
Berekeningen van Hold Period Return (HPR)
Formule van HPR
HPR = ((waarde einde periode - oorspronkelijke waarde) + inkomsten) / oorspronkelijke waarde) * 100
HPR (Boom) = ((200-93) +7) / 93 = 122.58%
HPR (Normaal) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (recessie) = ((4-93) +2) / 93 = -93.55%
Berekening van verwacht rendement
Formule van verwachte terugkeer
Verwacht rendement = (waarschijnlijkheid van giek * rendement van giek) + (waarschijnlijkheid van normaal * rendement van normaal) + (waarschijnlijkheid van recessie * rendement van recessie)
- Verwacht rendement = (0, 45 x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Verwacht rendement = 43.04%
Berekening van standaardafwijking
Formule van variantie
Variantie = (Waarschijnlijkheid van giek * (Rendement van giek - Totaal verwacht rendement) 2) + (Waarschijnlijkheid van Normaal * (Rendement van normaal - Totaal verwacht rendement) 2 ) + (Kans op recessie * (Rendement van recessie - Totaal verwacht rendement) 2)
- Variantie = 0, 45 (122, 58– (43.04)) 2 + 0, 35 (18, 82– (43.04)) 2 + 0, 20 (-93.55– (43.04)) 2
- Variantie = 6783.65
Formule van standaardafwijking
Standaardafwijking is Square Root of Variance
Standaardafwijking = √ Variantie
- Standaardafwijking = √6783.65
- Standaardafwijking = 82, 36%
Berekening van het verwachte rendement en de standaarddeviatie van een half belegde portefeuille in bedrijf A en de helft in bedrijf B.
Standaardafwijking van bedrijf A = 29, 92%
Standaardafwijking van bedrijf B = 82, 36%
Gewicht van bedrijf A = 0, 50
Gewicht van bedrijf B = 0, 50
De formule van Standaarddeviatie van Portfolio
Standaardafwijking van de portefeuille = (gewicht van bedrijf A * verwacht rendement van bedrijf A) + ((gewicht van bedrijf B * verwacht rendement van bedrijf B)
- Standaardafwijking van de portefeuille = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Standaardafwijking van de portefeuille = 56, 14%
Analyse
De standaarddeviatie van de portefeuille is lager dan die van beide aandelen omdat de aandelen in verschillende aandelen zijn gediversifieerd. Diversificatie leidt tot een vermindering van het risico, tenzij er een perfecte correlatie bestaat tussen het rendement op portefeuillebeleggingen.
Conclusie - standaardafwijkingsvoorbeelden
De standaarddeviatie meet de spreiding van de gegevensset ten opzichte van het gemiddelde. Het wordt berekend als de vierkantswortel van variantie. Hoe groter de standaardafwijking van de beveiliging, des te groter zal de variantie tussen elk van de prijs en het gemiddelde zijn, wat aantoont dat de prijsklasse groot is. De bovengenoemde voorbeelden zijn enkele voorbeelden van standaarddeviatie op verschillende manieren. Er zijn ook verschillende andere voorbeelden die aantonen dat de standaarddeviatie kan worden berekend met behulp van andere gegevens.
Aanbevolen artikelen
Dit is een leidraad geweest voor de standaardafwijkingsvoorbeelden. Hier bespreken we de verschillende voorbeelden van standaarddeviatie samen met een gedetailleerde uitleg . U kunt ook de volgende artikelen bekijken voor meer informatie -
- Voorbeeld vaste kosten
- Variabel kostenvoorbeeld
- Kwantitatief onderzoeksvoorbeeld
- Monopolistische concurrentie voorbeelden