
Inleiding tot functies in R
De functie is gedefinieerd als een set instructies om elke specifieke logische taak uit te voeren en te volbrengen. Functie heeft enkele invoerparameters nodig die argumenten worden genoemd om die taak uit te voeren. Functies helpen bij het breken van de code, in eenvoudiger stukken door het logisch te orkestreren, wat gemakkelijker te lezen en te begrijpen is. In dit onderwerp gaan we meer te weten over functies in R.
Hoe functies te schrijven in R?
Om de functie in R te schrijven, is hier de syntaxis:
Fun_name <- function (argument) (
Function body
)
Hier kan men zien dat "functie" specifiek gereserveerd woord wordt gebruikt in R, om elke functie te definiëren. De functie neemt invoer in de vorm van argumenten. De hoofdtekst is een set logische instructies die worden uitgevoerd op basis van argumenten en retourneert vervolgens de uitvoer. "Fun_name" is de naam die aan de functie wordt gegeven en waarmee deze overal in het R-programma kan worden opgeroepen.
Laten we een voorbeeld bekijken, dat helderder zal zijn in het begrijpen van het concept van functie in R.
R code
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
output:
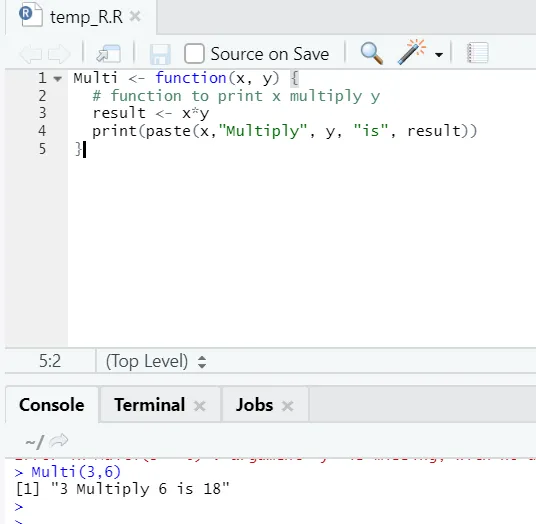
Hier hebben we de functienaam "Multi" gecreëerd, die twee argumenten als invoer gebruikt en de vermenigvuldigde uitvoer levert. Het eerste argument is x en het tweede argument is y. Zoals u ziet, hebben we de functie "Multi" genoemd. Hier kunnen, als iemand wil, argumenten ook worden ingesteld op de standaardwaarde.
Verschillende soorten functies in R
Verschillende R-functies met syntaxis en voorbeelden (ingebouwd, wiskunde, statistisch, enz.)
1) Ingebouwde functie -
Dit zijn de functies die bij R horen om een specifieke taak aan te pakken door een argument als invoer te nemen en een uitvoer te geven op basis van de gegeven invoer. Laten we hier enkele belangrijke algemene functies van R bespreken:
a) Sorteren: gegevens kunnen van de sortering in oplopende of aflopende volgorde zijn. Gegevens kunnen zijn of een vector van continu variabele of factor variabele.
Syntaxis:

Hier is de uitleg van de parameters:
- x: Dit is een vector van de continue variabele of factorvariabele
- aflopend: dit kan worden ingesteld op Waar / Onwaar om de volgorde te regelen door op te lopen of af te dalen. Standaard is het FALSE`.
- last: als de vector NA-waarden heeft, moet deze als laatste worden geplaatst of niet
R-code en uitvoer:
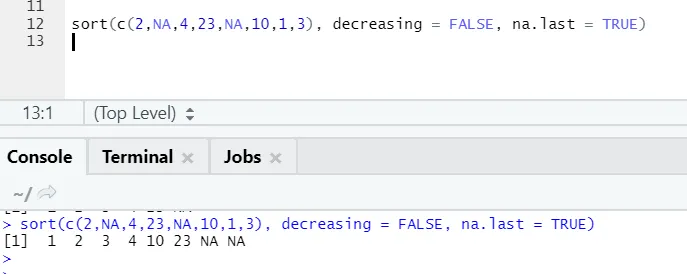
Hier kan men opmerken hoe "NA" -waarden aan het einde worden uitgelijnd. Omdat onze parameter na.last = True waar was.
b) Seq: het genereert een reeks van het nummer tussen twee opgegeven nummers.
Syntaxis
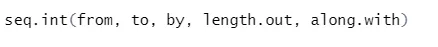
Hier is de uitleg van de parameters:
- van, naar begin- en eindwaarde van de reeks.
- door: Toename / kloof tussen twee opeenvolgende nummers in volgorde
- length.out: de vereiste lengte van de reeks.
- Along.with: verwijst naar de lengte van de lengte van dit argument
R-code en uitvoer:
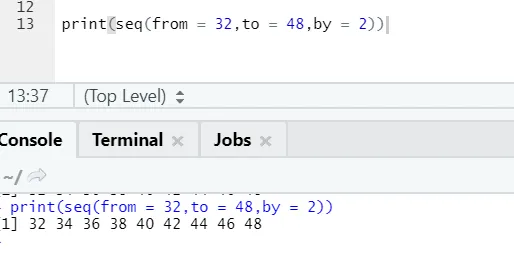
Hier kan men opmerken dat de gegenereerde reeks een toename van 2 heeft omdat door is gedefinieerd als 2.
c) Toupper, tolower: De twee functies: toupper en tolower zijn functies die op de string worden toegepast om de letters van de letters in zinnen te wijzigen.
R-code en uitvoer:
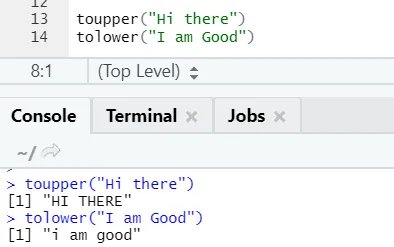
Men kan opmerken, hoe de letters van letters veranderen wanneer toegepast op de functie.
d) Rnorm: dit is een ingebouwde functie die willekeurige getallen genereert.
R-code en uitvoer:
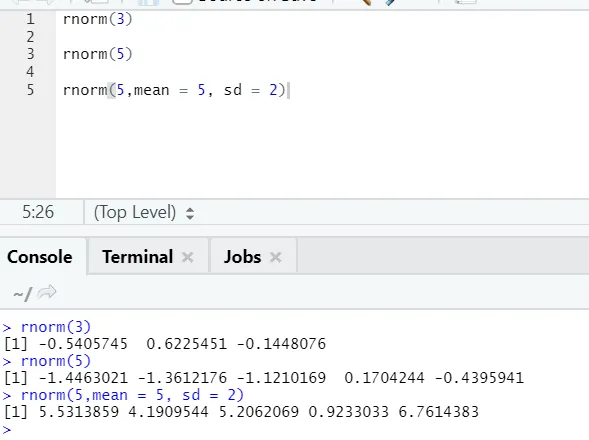
De functie rnorm neemt het eerste argument dat zegt hoeveel getallen moeten worden gegenereerd.
e) Rep: deze functie repliceert de waarde zo vaak als opgegeven.
R-syntaxis: rnorm (x, n)
Hier staat x voor te repliceren waarde en n voor het aantal keren dat het moet worden gerepliceerd.
R-code en uitvoer:
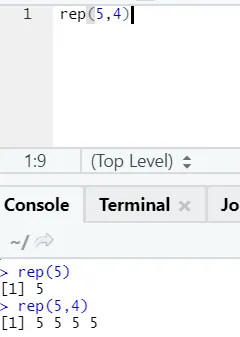
f) Plakken: deze functie is om tekenreeksen samen te voegen met een specifiek teken ertussen.
syntaxis
paste(x, sep = “”, collapse = NULL)
R code
paste("fish", "water", sep=" - ")
R uitgang:
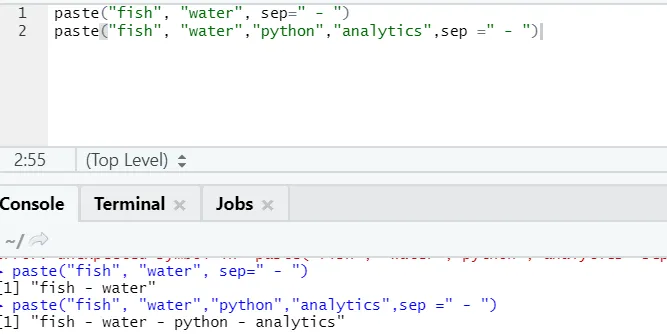
Zoals u kunt zien, kunnen we ook meer dan twee tekenreeksen plakken. Sep is dat specifieke karakter dat we tussen strings hebben toegevoegd. Standaard is sep spatie.
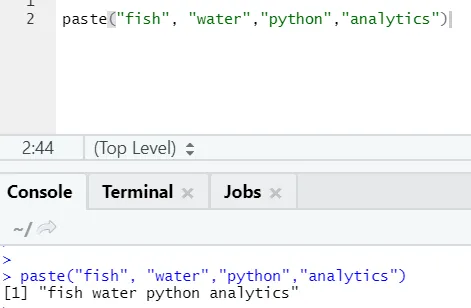
Nog een soortgelijke functie bestaat zoals deze, waarvan iedereen op de hoogte moet zijn, paste0.
De functie paste0 (x, y, collapse) werkt vergelijkbaar met paste (x, y, sep = "", collapse)
Zie het onderstaande voorbeeld:
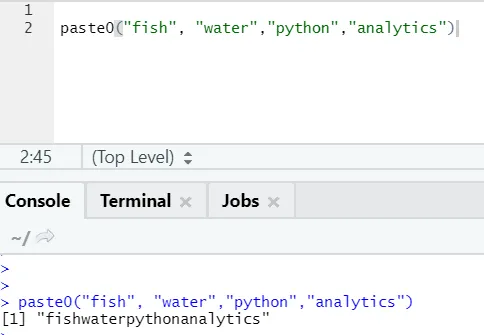
In eenvoudige woorden, om paste en paste0 samen te vatten:
Paste0 is sneller dan plakken als het gaat om het samenvoegen van tekenreeksen zonder scheidingsteken. As paste zoekt altijd naar "sep" en dat is standaard ruimte erin.
g) Strsplit: deze functie is om de string te splitsen. Laten we de eenvoudige gevallen bekijken:
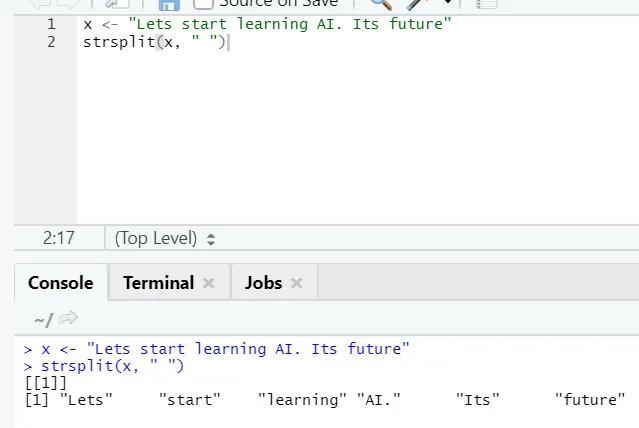
h) Rbind: de functie rbind helpt bij het kammen van vectoren met hetzelfde aantal kolommen, de ene boven de andere.
Voorbeeld
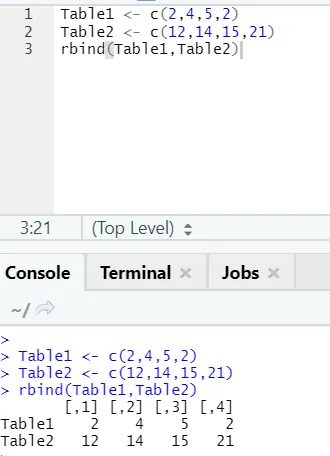
i) cbind: dit combineert vectoren met hetzelfde aantal rijen naast elkaar.
Voorbeeld
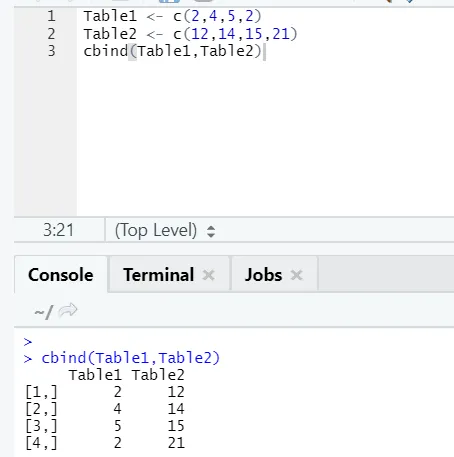
Als het aantal rijen niet overeenkomt, ziet u hieronder de fout:

Zowel cbind als rbind helpt bij gegevensmanipulatie en hervorming.
2) Wiskundige functie -
R biedt een breed scala aan wiskundige functies. Laten we er enkele in detail bekijken:
a) Sqrt: deze functie berekent de vierkantswortel van een nummer of numerieke vector.
R-code en uitvoer:
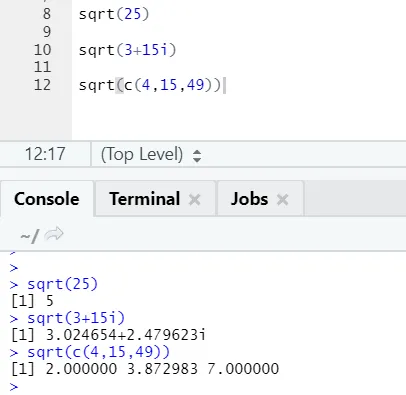
Men kan zien hoe de vierkantswortel van een getal, een complex getal en een reeks numerieke vector is berekend.
b) Exp: deze functie berekent de exponentiële waarde van een getal of een numerieke vector.
R-code en uitvoer:
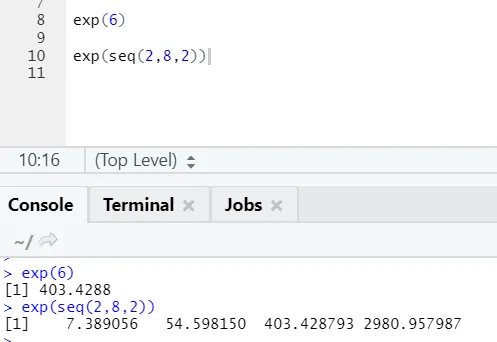
c) Cos, Sin, Tan: dit zijn trigonometriefuncties die hier in R zijn geïmplementeerd.
R-code en uitvoer:
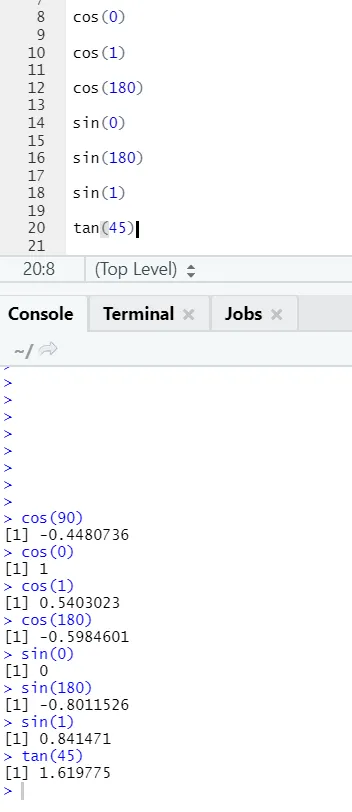
d) Abs: deze functie retourneert de absoluut positieve waarde van een getal.
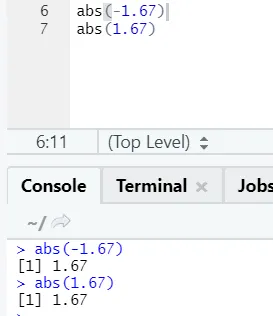
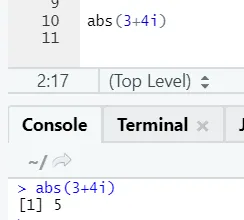
Zoals u ziet, wordt het negatieve of positieve getal van een getal in zijn absolute vorm geretourneerd. Laten we het voor een complex getal bekijken:
e) Log: dit is om de logaritme van een nummer te vinden.
Hier is het voorbeeld dat hieronder wordt getoond:
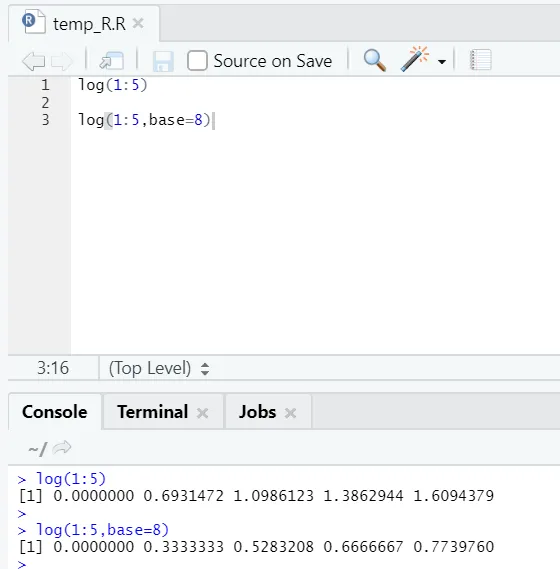
Hier krijgt men de flexibiliteit om de basis te veranderen, per eis.
f) Cumsum: dit is een wiskundige functie die cumulatieve sommen geeft. Hier is het onderstaande voorbeeld:
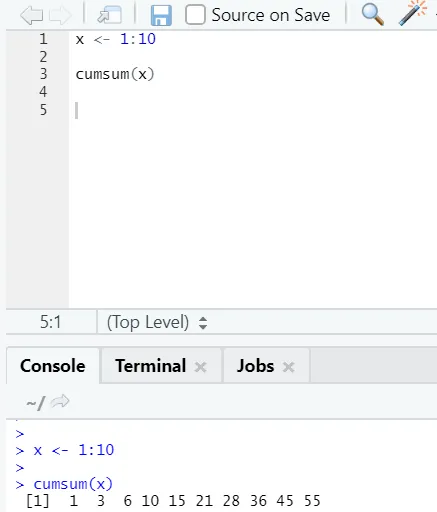
g) Cumprod: net als de wiskundige functie van Cumsum hebben we cumprod waar cumulatieve vermenigvuldiging plaatsvindt.
Zie het onderstaande voorbeeld:
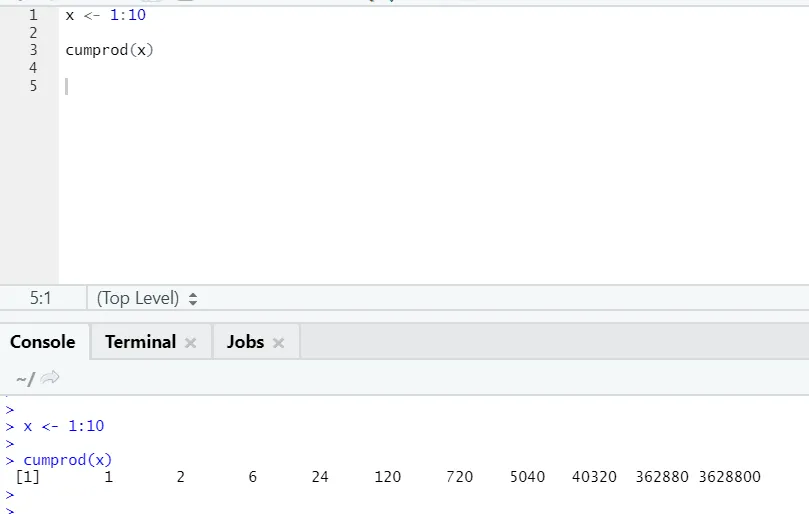
h) Max, Min: dit helpt u bij het vinden van de maximale / minimale waarde in de reeks getallen. Zie hieronder de voorbeelden die hiermee verband houden:
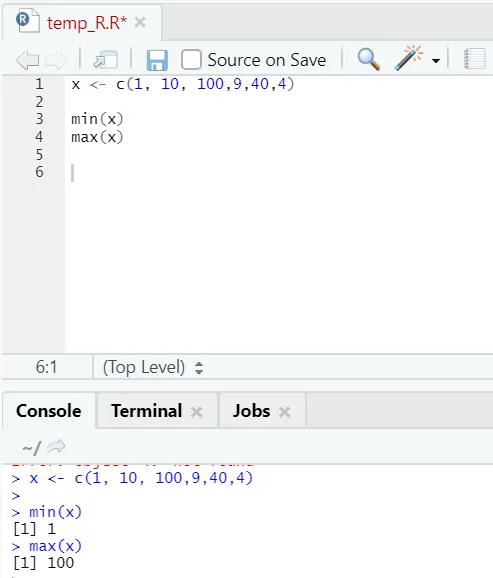
i) Plafond: het plafond is een wiskundige functie die het kleinste van het gehele getal retourneert dat hoger is dan opgegeven.
Laten we een voorbeeld bekijken:
plafond (2, 67)
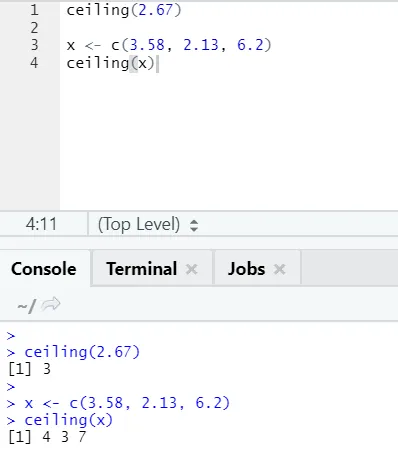
Zoals u kunt zien, wordt het plafond zowel op een nummer als op een lijst toegepast en is de uitvoer het kleinst van het volgende hogere gehele getal.
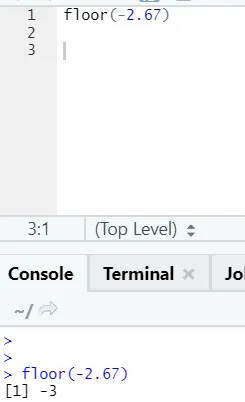
j) Verdieping: de verdieping is een wiskundige functie die het kleinste geheel getal van het opgegeven getal retourneert.
Het onderstaande voorbeeld helpt u het beter te begrijpen:
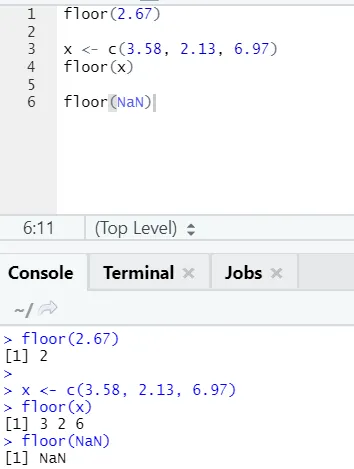
Het werkt ook op dezelfde manier voor negatieve waarden. Kijk alsjeblieft:
3) Statistische functies -
Dit zijn de functies die de gerelateerde waarschijnlijkheidsverdeling beschrijven.
a) Mediaan: dit berekende de mediaan uit de reeks getallen.
Syntaxis
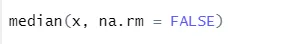
R-code en uitvoer:
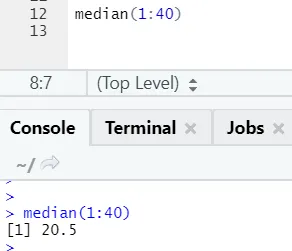
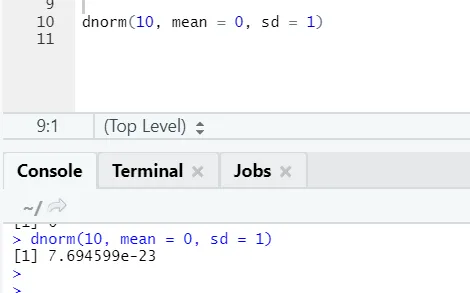
b) Dnorm: dit verwijst naar de normale verdeling. De functie dnorm geeft de waarde van de waarschijnlijkheidsdichtheidsfunctie terug, voor de normale verdeling gegeven parameters voor x, μ en σ.
R-code en uitvoer:
c) Cov: Covariantie vertelt of twee vectoren positief, negatief of volledig niet-gerelateerd zijn.
R code
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
R uitgang:
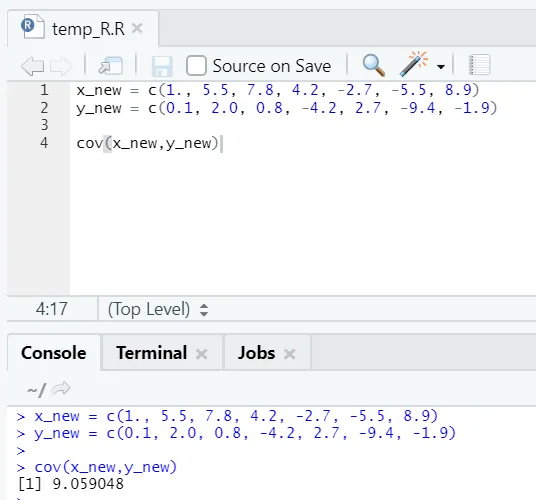
Zoals je kunt zien, zijn twee vectoren positief gerelateerd, wat betekent dat beide vectoren in dezelfde richting bewegen. Als de covariantie negatief is, betekent dit dat x en y omgekeerd evenredig zijn en dus in de tegenovergestelde richting bewegen.
d) Cor: Dit is een functie om de correlatie tussen vectoren te vinden. Het geeft feitelijk de associatiefactor tussen de twee vectoren die bekend staat als de "correlatiecoëfficiënt". Correlatie voegt een graadfactor toe aan covariantie. Als twee vectoren positief gecorreleerd zijn, zal de correlatie u ook vertellen in hoeverre ze positief gerelateerd zijn.
Deze drie soorten methoden die kunnen worden gebruikt om een correlatie tussen twee vectoren te vinden:
- Pearson correlatie
- Kendall-correlatie
- Spearman-correlatie
In eenvoudig R-formaat ziet het eruit als:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Hier zijn x en y vectoren.
Laten we het praktische voorbeeld van correlatie over een ingebouwde gegevensset bekijken.
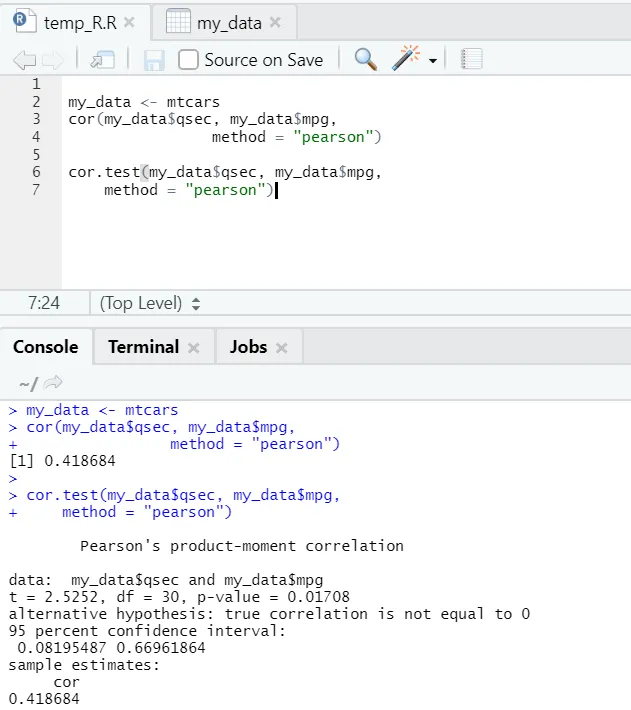
Hier ziet u dus dat de functie "cor ()" de correlatiecoëfficiënt 0, 41 gaf tussen "qsec" en "mpg". Er is echter nog een functie getoond, dat wil zeggen “cor.test ()” die niet alleen de correlatiecoëfficiënt vertelt, maar ook de daaraan gerelateerde p-waarde en t-waarde. Interpretatie wordt veel eenvoudiger met de cor.test-functie.
Hetzelfde kan worden gedaan met de andere twee correlatiemethoden:
R-code voor de Pearson-methode:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
R-code voor Kendall-methode:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
R-code voor Spearman-methode:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
De correlatiecoëfficiënt varieert tussen -1 en 1.
Als de correlatiecoëfficiënt negatief is, betekent dit dat wanneer x toeneemt, y afneemt.
Als de correlatiecoëfficiënt nul is, betekent dit dat er geen verband bestaat tussen x en y.
Als de correlatiecoëfficiënt positief is, betekent dit dat wanneer x toeneemt, y ook de neiging heeft toe te nemen.
e) T-test: de T-test vertelt u of twee gegevenssets afkomstig zijn van dezelfde (uitgaande) normale distributies of niet.
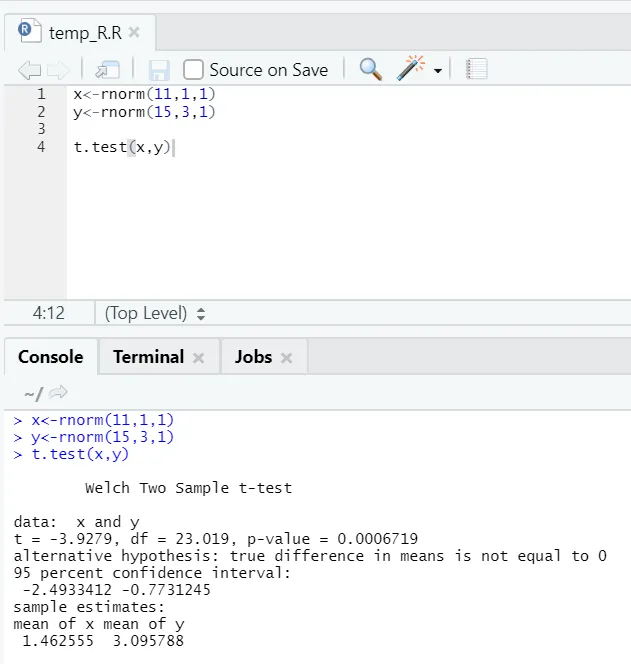
Hier moet u de nulhypothese verwerpen dat de twee gemiddelden gelijk zijn omdat de p-waarde kleiner is dan 0, 05.
Dit weergegeven exemplaar is van het type: niet-gepaarde gegevenssets met ongelijke varianties. Evenzo kan worden geprobeerd met de gepaarde gegevensset.
f) Eenvoudige lineaire regressie: dit toont de relatie tussen de voorspeller / onafhankelijke en respons / afhankelijke variabele.
Een eenvoudig praktisch voorbeeld zou het voorspellen van het gewicht van een persoon kunnen zijn als de lengte bekend is.
R syntaxis
lm(formula, data)
Hier geeft de formule de relatie weer tussen uitvoer, dwz y en invoervariabele iex. Gegevens vertegenwoordigen de gegevensset, waarop de formule moet worden toegepast.
Laten we een praktisch voorbeeld bekijken, waarbij het vloeroppervlak de invoervariabele is en huur de uitvoervariabele is.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
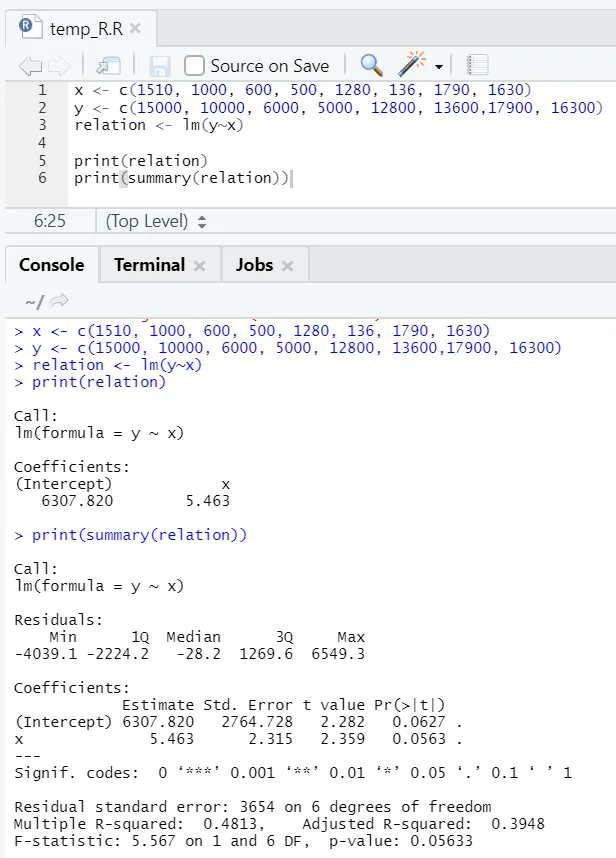
Hier is de P-waarde niet minder dan 5%. Daarom kan de nulhypothese niet worden afgewezen. Er is niet veel betekenis om de relatie tussen het vloeroppervlak en de huur te bewijzen.
Hier is de R-kwadraatwaarde 0, 4813. Dat betekent dat slechts 48% van de variantie in de uitvoervariabele kan worden verklaard door de invoervariabele.
Laten we zeggen dat we nu moeten voorspellen voor een waarde van de vloeroppervlakte, op basis van het hierboven gemonteerde model.
R code
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
R uitgang:
Na het uitvoeren van de bovenstaande R-code ziet de uitvoer er als volgt uit:
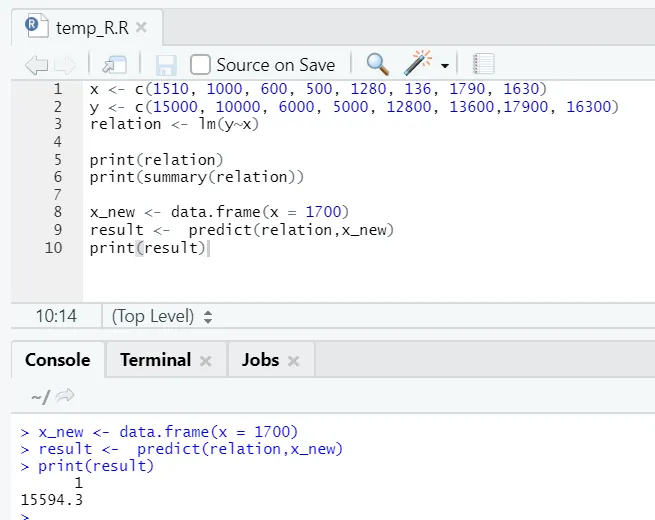
Men kan regressie passen en visualiseren. Hier is de R-code daarvoor:
# Geef het png-kaartbestand een naam.
png(file = "LinearRegressionSample.png.webp")
# Zet de grafiek uit.
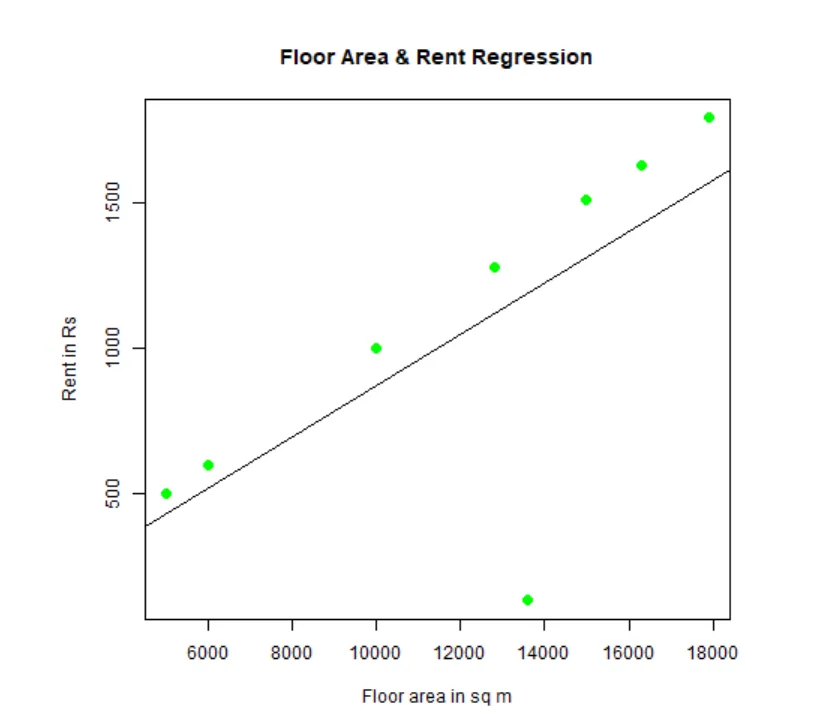
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Bewaar het bestand.
dev.off()
Deze grafiek "LinearRegressionSample.png.webp" wordt gegenereerd in uw huidige werkmap.
g) Chi-Square-test
Dit is een statistische functie in R. Deze test heeft zijn betekenis om te bewijzen of de correlatie bestaat tussen twee categorische variabelen.
Deze test werkt ook zoals elke andere statistische test was gebaseerd op p-waarde, men kan de nulhypothese accepteren of verwerpen.
R syntaxis
chisq.test(data), /code>
Laten we er een praktisch voorbeeld van bekijken.
R code
# Laad de bibliotheek.
library(datasets)
data(iris)
# Maak een dataframe van de hoofdgegevensset.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Maak een tabel met de benodigde variabelen.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Voer de Chi-Square-test uit.
print(chisq.test(iris.data))
R uitgang:
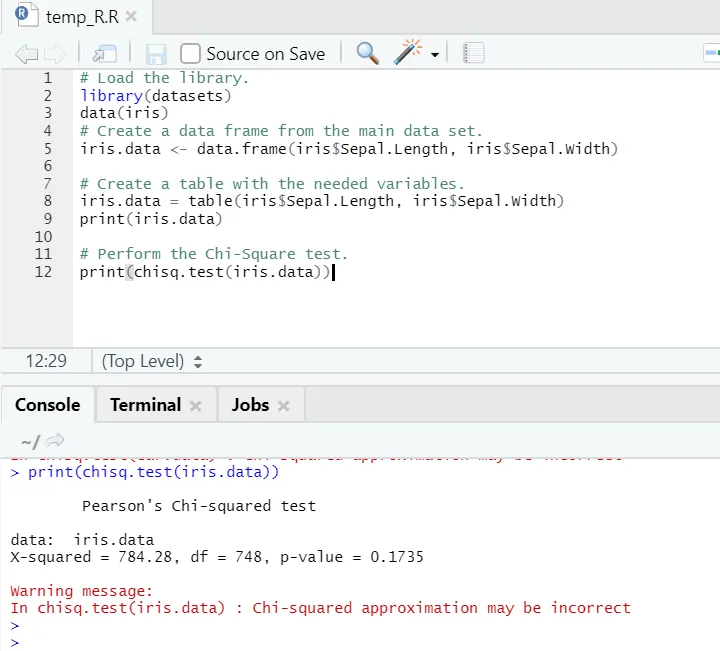
Zoals je kunt zien, is de chikwadraat-test uitgevoerd over een iris-gegevensset, gezien de twee variabelen 'Sepal. Lengte 'en' Sepal.Width '.
De p-waarde is niet minder dan 0, 05, vandaar dat er geen correlatie bestaat tussen deze twee variabelen. Of we kunnen zeggen dat deze twee variabelen niet van elkaar afhankelijk zijn.
Conclusie
Functies in R zijn eenvoudig, gemakkelijk te plaatsen, gemakkelijk te begrijpen en toch zeer krachtig. We zagen een verscheidenheid aan functies die worden gebruikt als onderdeel van de basisprincipes in R. Zodra men vertrouwd raakt met deze hierboven besproken functies, kan men andere soorten functies verkennen. Functies helpen u om uw code eenvoudig en beknopt uit te voeren. Functies kunnen worden ingebouwd of door de gebruiker worden gedefinieerd, alles hangt af van de behoefte bij het oplossen van een probleem. Functies geven een programma een goede vorm.
Aanbevolen artikelen
Dit is een gids voor Functies in R. hier bespreken we hoe u Functies in R en verschillende soorten Functies in R kunt schrijven met syntaxis en voorbeelden. U kunt ook het volgende artikel bekijken voor meer informatie -
- R-snaarfuncties
- SQL String-functies
- T-SQL String-functies
- PostgreSQL-stringfuncties