Gewogen gemiddelde formule (inhoudsopgave)
- Gewogen gemiddelde formule
- Gewogen gemiddelde calculator
- Gewogen gemiddelde formule in Excel (met Excel-sjabloon)
Gewogen gemiddelde formule
De formule voor het berekenen van gewogen gemiddelde is als volgt:
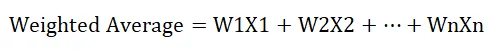
Waar,
- W geeft relatief gewicht aan (in%)
- X geeft waarde aan
Voorbeelden van gewogen gemiddelde formule
Laten we een paar voorbeelden bekijken om de gewogen gemiddelde formule te begrijpen:
Voorbeeld 1
Laten we aannemen dat Anand het geld in de volgende verhouding heeft geïnvesteerd: 40% in investering A, 20% in investering B en 40% in investering C. Deze investeringen hebben een rendement als volgt: Investering A als 15%, Investering B als 10 % en investering C respectievelijk 20%. We moeten een gewogen gemiddelde berekenen voor de rendementen die Anand zou ontvangen.
Hier,
- We hebben relatieve gewichten voor de beleggingen A, B en C als respectievelijk 40%, 20% en 40%.
- En Waarde (rendement) voor de investeringen A, B & C als respectievelijk 15%, 10% en 20%.
Door de Gewogen Gemiddelde Formule te gebruiken, krijgen we-
- Gewogen gemiddelde = W1 X1 + W2 X2 + …… + Wn Xn
- Gewogen gemiddelde = 40% * 15% + 20% * 10% + 40% * 20%
- Gewogen gemiddelde = 16%
Dit geeft aan dat Anand 16% gewogen gemiddelde rendementen ontvangt van de Investeringen A, B & C.
Voorbeeld 2
Laten we aannemen dat Anand zich heeft ingeschreven voor een wiskundecursus, zijn eindcijfer wordt bepaald op basis van de volgende categorieën: tests 30%, eindexamen 40%, quizzen 15% en huiswerk 15%.
Anand scoort het volgende cijfer in elke categorie: Tests-80, eindexamen-65, quizzen-85, huiswerk-90. Nu moeten we het algemene cijfer van Anand achterhalen.
Om een gewogen gemiddelde met percentages te berekenen, moet elke categoriewaarde eerst met zijn percentage worden vermenigvuldigd. Dan moeten al deze nieuwe waarden bij elkaar worden opgeteld.
Hier,
We hebben relatieve gewichten voor de volgende categorieën als volgt:
- Tests 30%
- Eindexamen 40%
- quizzen 15%
- huiswerk 15%
En Waarde (markeringen) voor de categorieën als
- Tests-80
- Eindexamen 65,
- quiz-85
- huiswerk-90
Door de Gewogen Gemiddelde Formule te gebruiken, krijgen we-
- Gewogen gemiddelde = W1 X1 + W2 X2 + …… + WnXn
- Gewogen gemiddelde = (30% * 80) + (40% * 65) + (15% * 85) + (15% * 90)
- Gewogen gemiddelde = 76.25 of 76%
Dit toont aan dat het algemene cijfer van Anand 76% is.
Voorbeeld # 3
Laten we aannemen dat Jagriti geld heeft geïnvesteerd in aandelen van verschillende bedrijven. Jagriti-portefeuille omvat 30% in voorraad A, 15% in voorraad B, 30% in voorraad C en de resterende 25% in voorraad D. Het verwachte rendement volgens de huidige marktsituatie op deze aandelen is als volgt: Rendement op voorraad A is 15%, rendement op voorraad B is 12%, rendement op voorraad C is 17% en rendement op voorraad D is 16% respectievelijk. Jagriti wil haar gemiddelde rendement op de portefeuille berekenen volgens de huidige marktsituatie.
Hier,
- We hebben relatieve gewichten van de aandelen in de portefeuille als volgt: A, B, C & D als respectievelijk 30%, 15%, 30% en 25%.
- En Waarde (rendement) voor de aandelen als volgt: A, B, C & D als respectievelijk 15%, 12%, 17% en 16%.
Door de Gewogen Gemiddelde Formule te gebruiken, krijgen we-
- Gewogen gemiddelde = W1 X1 + W2 X2 + W3 X3 + W4 X4 …… + Wn Xn
- Gewogen gemiddelde = (30% * 15%) + (15% * 12%) + (30% * 17%) + (25% * 16%)
- Gewogen gemiddelde = 0.154 of 15, 4%
Dit toont aan dat Jagriti 15, 4% gemiddeld rendement zal ontvangen uit de portefeuille van aandelen A, B, C en D.
Verklaring van de gewogen gemiddelde formule
De gewogen gemiddelde formule wordt gebruikt voor het berekenen van de gemiddelde waarde voor een bepaalde reeks getallen met verschillende niveaus van relevantie. De gewichten moeten worden weergegeven in termen van totale relevantie als een percentage. De genomen gewichten moeten gelijk zijn aan 100% of 1.
Om de gewogen gemiddelde formule te berekenen, hebben we relatieve weging en waarde nodig.
De eerste component is Relatieve weging en de tweede component is waarde-invoer. Om het gewogen gemiddelde te berekenen, moeten we een specifiek gewicht hebben voor elke variabele als waarde en het gewicht moet gelijk zijn aan 100%.
Betekenis en gebruik van gewogen gemiddelde formule
Het gewogen gemiddelde wordt in verschillende financiële formules gebruikt. Enkele voorbeelden van gewogen gemiddelde bèta en gewogen gemiddelde kapitaalkosten (WACC).
We zijn bekend met het idee om het athematische gemiddelde of gemiddelde te vinden voor een reeks items. We kunnen eenvoudig waarden van alle artikelen optellen en delen door het totale aantal artikelen om het gemiddelde te berekenen. Dit werkt alleen als alle items even zwaar zijn gewogen. Voor het berekenen van de gemiddelde maandelijkse mobiele facturen voor een jaar, kunnen we bijvoorbeeld de totale gefactureerde bedragen voor de afgelopen twaalf maanden optellen en delen door twaalf, dan kunnen we een ruw idee krijgen voor de gemiddelde betaalde factuur, omdat de mobiele telefoon factuurcyclus is ongeveer voor dezelfde periode, dwz één maand.
Stel dat u het huidige gemiddelde cursuscijfer in uw wiskundeles wilt berekenen. Meestal kennen de meeste klassen een ander gewicht toe aan examens dan aan huiswerkopdrachten, interne tests en wedstrijden. In dit geval moet u een gewogen gemiddelde berekenen, waarmee het specifieke gewicht voor elk onderwerp wordt berekend om uw cursuscijfer te berekenen.
Voorbeeld van enkele gevallen waarin een gewogen gemiddelde moet worden gebruikt in plaats van een eenvoudig gemiddelde. Eerste geval - Wanneer we een gemiddelde willen berekenen met verschillende percentagewaarden voor verschillende categorieën. Het bovenstaande voorbeeld van het cursuscijfer is een van de vergelijkbare gevallen. En ten tweede wanneer we een grote groep items hebben met een andere regelmaat.
Als een bedrijf een grote fluctuatie in de omzet heeft als gevolg van de productie van een seizoensproduct, kunnen ze de gewogen gemiddelde formule gebruiken. En het bedrijf wil het gemiddelde voor hun variabele uitgaven berekenen, dan kan het bedrijf de gewogen gemiddelde formule gebruiken en de omzet als het gewicht nemen om een beter inzicht te krijgen in hun uitgaven. En kunnen de hoeveelheid die ze produceren of verkopen vergelijken.
Gewogen gemiddelde calculator
U kunt de volgende gewogen gemiddelde calculator gebruiken
| W 1 | |
| X 1 | |
| W 2 | |
| X 2 | |
| W 3 | |
| X 3 | |
| W 4 | |
| X 4 | |
| Gewogen gemiddelde formule | |
| Gewogen gemiddelde formule = | W 1 * X 1 + W 2 * X 2 + W 3 * X 3 + W 4 * X 4 | |
| 0 * 0 + 0 * 0 + 0 * 0 + 0 * 0 = | 0 |
Gewogen gemiddelde formule in Excel (met Excel-sjabloon)
Hier zullen we hetzelfde voorbeeld doen van de formule Gewogen gemiddelde in Excel. Het is heel gemakkelijk en eenvoudig. U moet de twee ingangen opgeven, dwz relatieve gewichten en rendement.
U kunt het gewogen gemiddelde eenvoudig berekenen met behulp van de formule in de meegeleverde sjabloon.
wegingsgemiddelde rendementen van de investeringen A, B & C worden berekend als:

algemeen cijfer van Anand wordt berekend als:

gewicht Leeftijd gemiddelde rendementen uit de portefeuille van aandelen A, B, C en D worden berekend als:
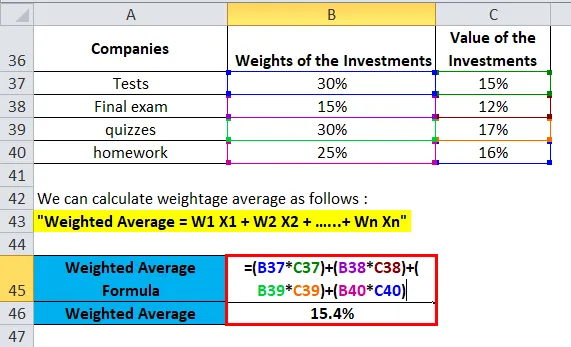
U kunt deze gewogen gemiddelde formule Excel-sjabloon hier downloaden - Gewogen gemiddelde formule Excel-sjabloon
Aanbevolen artikelen
Dit is een leidraad geweest voor een formule voor gewogen gemiddelde. Hier bespreken we het gebruik ervan samen met praktische voorbeelden. We bieden u ook een gewogen gemiddelde calculator met een downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Hoe de overheadratio te berekenen?
- Bereken equity multiplier met voorbeelden
- Gebruik van brutowinstmargeformule
- Handleiding voor de berekening van de omzet van de vorderingen