
Formule van foutmarge (inhoudsopgave)
- Formule van foutmarge
- Voorbeelden van de foutmargeformule (met Excel-sjabloon)
- Marge van fout formule rekenmachine
Formule van foutmarge
In de statistiek berekenen we het betrouwbaarheidsinterval om te zien waar de waarde van de gegevens van de steekproefstatistiek zal dalen. Het bereik van waarden die onder en boven de steekproefstatistiek in een betrouwbaarheidsinterval liggen, staat bekend als Foutmarge. Met andere woorden, het is in feite de mate van fouten in de steekproefstatistiek. Hoe hoger de foutmarge, hoe minder vertrouwen in de resultaten, omdat de mate van afwijking in deze resultaten zeer hoog is. Zoals de naam al doet vermoeden, is de foutmarge een reeks waarden boven en onder de werkelijke resultaten. Als we bijvoorbeeld een antwoord krijgen in een enquête waarbij 70% van de mensen "goed" heeft gereageerd en de foutenmarge 5% is, betekent dit dat in het algemeen 65% tot 75% van de bevolking denkt dat het antwoord "goed" is .
De formule voor foutmarge -
Margin of Error = Z * S / √n
Waar:
- Z - Z score
- S - Standaardafwijking van een populatie
- n - Steekproefgrootte
Een andere formule voor het berekenen van de foutmarge is:
Margin of Error = Z * √((p * (1 – p)) / n)
Waar:
- p - Sample Proportion (fractie van sample die een succes is)
Om de gewenste z-score te vinden, moet u het betrouwbaarheidsinterval van de steekproef kennen, omdat de Z-score daarvan afhankelijk is. Onderstaande tabel wordt gegeven om de relatie tussen een betrouwbaarheidsinterval en z-score te bekijken:
| Betrouwbaarheidsinterval | Z - Score |
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Zodra u het betrouwbaarheidsinterval kent, kunt u de bijbehorende z-waarde gebruiken en vanaf daar de foutmarge berekenen.
Voorbeelden van de foutmargeformule (met Excel-sjabloon)
Laten we een voorbeeld nemen om de berekening van de marge van fouten beter te begrijpen.
U kunt deze sjabloon voor foutmarge hier downloaden - sjabloon voor foutmargeFormule van foutmarge - Voorbeeld # 1
Laten we zeggen dat we een enquête houden om te zien wat de cijfer score is die universitaire studenten behalen. We hebben willekeurig 500 studenten geselecteerd en hun score gevraagd. Het gemiddelde daarvan is 2, 4 van de 4 en de standaardafwijking is 30%. Neem aan dat het betrouwbaarheidsinterval 99% is. Bereken de foutmarge.
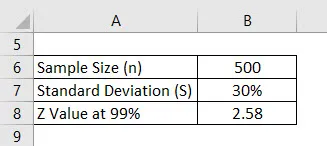
Oplossing:
Foutmarge wordt berekend met behulp van de onderstaande formule
Foutmarge = Z * S / √n
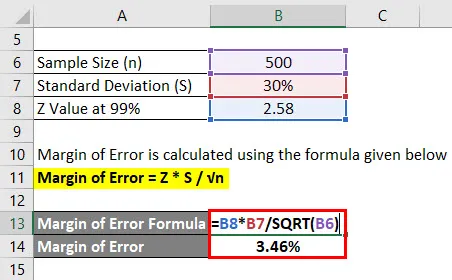
- Foutmarge = 2, 58 * 30% / √ (500)
- Foutmarge = 3, 46%
Dit betekent dat met 99% betrouwbaarheid het gemiddelde cijfer van studenten 2, 4 plus of min 3, 46% is.
Formule van foutmarge - Voorbeeld # 2
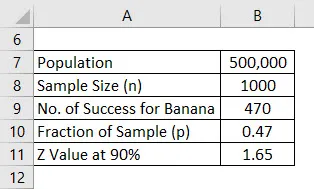
Stel dat u een nieuw gezondheidsproduct op de markt brengt, maar dat u niet weet welke smaak mensen lekker zullen vinden. Je bent in de war tussen de bananensmaak en de vanillesmaak en hebt besloten om een onderzoek uit te voeren. Uw populatie daarvoor is 500.000, wat uw doelmarkt is en daarom hebt u besloten om de mening van 1000 mensen te vragen en dat zal de steekproef zijn. Neem aan dat een betrouwbaarheidsinterval 90% is. Bereken de foutmarge.
Oplossing:
Toen de enquête klaar was, kwam je te weten dat 470 mensen van de bananensmaak hielden en 530 om vanillesmaak vroeg.
Foutmarge wordt berekend met behulp van de onderstaande formule
Foutmarge = Z * √ ((p * (1 - p)) / n)
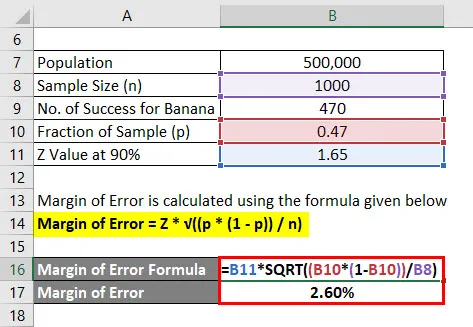
- Foutmarge = 1, 65 * √ ((0, 47 * (1 - 0, 47)) / 1000)
- Foutmarge = 2, 60%
We kunnen dus zeggen dat met 90% vertrouwen dat 47% van alle mensen van bananensmaak plus of min 2, 60% hield.
Uitleg
Zoals hierboven besproken, helpt de foutmarge ons te begrijpen of de steekproefomvang van uw enquête geschikt is of niet. In het geval dat de marifout te groot is, kan het zijn dat onze steekproefomvang te klein is en dat moeten we vergroten zodat de steekproefresultaten beter overeenkomen met de populatieresultaten.
Er zijn enkele scenario's waarbij de foutmarge niet veel gebruikt en ons niet helpt bij het volgen van de fout:
- Als de vragen van de enquête niet zijn ontworpen en niet helpen om het vereiste antwoord te krijgen
- Als de mensen die reageren op de enquête enige vooringenomenheid hebben ten aanzien van het product waarvoor de enquête wordt uitgevoerd, dan is het resultaat ook niet erg nauwkeurig
- Als de steekproef zelf de juiste vertegenwoordiger van de populatie is, zullen de resultaten ook in dat geval ver weg zijn.
Ook is een grote veronderstelling dat de bevolking normaal verdeeld is. Dus als de steekproefgrootte te klein is en de populatieverdeling niet normaal is, kan de z-score niet worden berekend en kunnen we de foutenmarge niet vinden.
Relevantie en gebruik van de foutmargeformule
Wanneer we steekproefgegevens gebruiken om een relevant antwoord voor de populatieset te vinden, is er enige onzekerheid en kans dat het resultaat kan afwijken van het werkelijke resultaat. De foutmarge zal ons vertellen dat wat het niveau van afwijking is, er de voorbeelduitvoer is. We moeten de foutmarge minimaliseren, zodat onze steekproefresultaten het werkelijke verhaal van populatiegegevens weergeven. Dus verlaag de foutmarge, beter zullen de resultaten zijn. De foutmarge vult de statistische informatie waarover we beschikken aan en vult deze aan. Als bijvoorbeeld uit een enquête blijkt dat 48% van de mensen er de voorkeur aan geeft om in het weekend thuis tijd door te brengen, kunnen we niet zo precies zijn en ontbreken er enkele elementen in die informatie. Toen we hier een foutmarge introduceerden, zeg 5%, dan zal de uitkomst worden geïnterpreteerd als 43-53% mensen vonden het een leuk idee om thuis te zijn tijdens het weekend, wat volkomen logisch is.
Marge van fout formule rekenmachine
U kunt de volgende foutmargecalculator gebruiken
| Z | |
| S | |
| √n | |
| Foutmarge | |
| Foutmarge | = |
|
|
Aanbevolen artikelen
Dit is een leidraad geweest voor de formule van de foutmarge. Hier bespreken we hoe de foutmarge te berekenen, samen met praktische voorbeelden. We bieden ook een foutmargecalculator met downloadbare Excel-sjabloon. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Handleiding voor lineaire afschrijvingsformule
- Voorbeelden van de verdubbelingstijdformule
- Hoe afschrijving te berekenen?
- Formule voor centrale limietstelling
- Altman Z Score | Definitie | Voorbeelden
- Afschrijvingsformule | Voorbeelden met Excel-sjabloon