
Inleiding tot wiskundige functies in C
Dit artikel geeft een overzicht van de verschillende wiskundige functies die worden gebruikt in C-programmeertalen met werkende code-afbeelding. Computers maken enorme wiskundige berekeningen en analyses van enorme aantallen, daarvoor hebben we wiskundige functies in C gebruikt. Voordat we beginnen, moeten we weten dat de C-talen header / bibliotheek genaamd Math.h gebruiken voor verschillende wiskundige functies. Dit helpt bij het berekenen van goniometrische bewerkingen, logaritmen, absolute waarden, vierkantswortels. Laten we dus de verschillende soorten functies verkennen die in deze bibliotheek worden gebruikt. Al deze functies nemen het dubbele als gegevenstype en retourneren hetzelfde.
Verschillende wiskundige functies in C
Laten we de verschillende functies bekijken die zijn gedefinieerd in wiskunde. H en de wiskundebibliotheek is onderverdeeld in drie hoofdtypen: trigonometrische functies, wiskundige functies, log- / expofuncties. Om de onderstaande functies te implementeren, is het verplicht om of in de code op te nemen.
1. verdieping (dubbel a)
Deze functie retourneert de grootste gehele waarde niet groter dan 'a' waarde. Het rondt een waarde af en geeft als resultaat een dubbele waarde. Het gedraagt zich anders voor negatieve getallen, omdat deze naar het volgende negatieve getal afronden.
Bijv: verdieping (7.2) is 7.0
verdieping (-7.2) is -8.0
Voorbeeld:
Dit programma illustreert hoe de vloer te berekenen voor de aangegeven waarde en rondt af naar de volgende waarde 10.
#include
#include
int main()
(
double f= -9.33;
int final;
final = floor(f);
printf("Floor value of %.2f = %d", f, final);
return 0;
)
Output:

2. plafond ()
Syntaxis:
double ceil (double b)
Deze functie retourneert de kleinste gehele waarde die groter is dan of gelijk is aan b en rondt de waarde naar boven af. Voor een negatieve waarde beweegt deze naar links. Voorbeeld 3.4 geeft als resultaat -3 de uitvoer.
Voorbeeld:
Dit programma verklaart door invoer te nemen in het float-argument en geeft de plafondwaarde terug.
#include
#include
int main()
(
float n, ceilVal;
printf(" Enter any Numeric element : ");
scanf("%f", &n);
ceilVal = ceil(n);
printf("\n The Value of %.2f = %.4f ", n, ceilVal);
return 0;
)
Output:

3. Sqrt ()
Deze functie retourneert de vierkantswortel van een opgegeven getal.
Syntaxis:
sqrt( arg)
Voorbeeld:
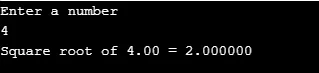
De onderstaande code verklaart de meest bekende wiskundige functie sqrt () door 'n' waarden te nemen om de vierkantswortel te berekenen voor de verschillende 'n' waarden.
#include
#include
int main()
(
double n, output;
printf("Enter a number\n");
scanf("%lf", &n);
output = sqrt(n);
printf("Square root of %.2lf = %f", n, output);
return 0;
Output:
4. ronde ()
Deze functie rondt de dichtstbijzijnde waarde van een gegeven invoer af. Het gooit de fout weg als de waarde te groot is. Andere functies zoals lround (), llround () rondt ook het dichtstbijzijnde gehele getal af.
Syntaxis:
int round(arg)
Voorbeeld:
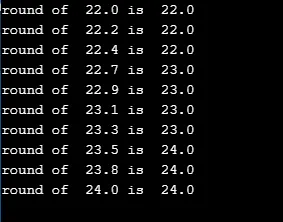
De onderstaande code is heel eenvoudig en wordt afgerond op de dichtstbijzijnde 'r'-waarde in de for-lus.
#include
#include
int main ()
(
for(double r=110;r<=120;r+=1.1)
printf("round of %.1lf is %.1lf\n", r/5.0, round(r/5.0));
return 0;)
Output:
5. kracht ()
Deze functie keert terug naar vermogen voor het gegeven nummer (a b ). Het retourneert een verhoogde naar de macht van b, die twee parameters base en exponent heeft.
Voorbeeld:
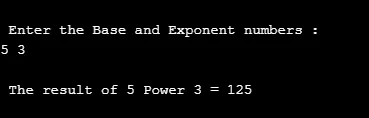
In de onderstaande broncode laten we een gebruiker een invoerwaarde invoeren om de kracht van de gegeven twee argumenten te berekenen.
#include
#include
int main()
(
int r, ba, expr;
printf("\n Enter the Base and Exponent numbers : \n");
scanf("%d %d", &ba, &expr);
r = pow(ba, expr);
printf("\n The result of %d Power %d = %d ", ba, expr, r);
return 0;
)
output:
6. trun ()
Deze functie helpt bij het afkappen van de gegeven waarde. Het geeft gehele waarden terug. Voor het afkappen van zwevende en dubbele waarden truncf (), wordt truncl () gebruikt.
Syntaxis:
double trunc(a);
Voorbeeld:
Onder de broncode zijn twee invoerwaarden a, b nodig om de dubbele waarden in te korten.
#include
#include
void main() (
double m, n, a, b;
a = 56.16;
b = 85.74;
m = trunc(a);
n = trunc(b);
printf("The value of a: %lf\n", m);
printf("The value of a: %lf\n", n);
)
Output:

7. fmod ()
Deze functie retourneert de rest voor de gegeven twee invoerwaarden wanneer m gedeeld door n.
Syntaxis:
double fmod(double I, double j)
Voorbeeld:
In het onderstaande voorbeeld zijn twee waarden van de gebruiker nodig om de rest te berekenen met de functie fmod ().
#include
#include
int main()(
double fiN;
double secN;
double n;
printf("Enter the first number : ");
scanf("%lf", &fiN);
printf("Enter the second number : ");
scanf("%lf", &secN);
printf("fmod(firstNumber, secondNumber) is %lf \n", fmod(fiN, secN));
)
Output:

Goniometrische functies
Hieronder staan de verschillende functies van Trigonometrische:
1. sin ()
Deze ingebouwde functie geeft sinuswaarde van het gegeven getal, berekent waarden met drijvende komma. asin () berekent boog, voor hyperbolisch is het sinh ().
Syntaxis:
return type sin(y);
y retourneert de waarde in radialen en het retourtype neemt het dubbele.
Voorbeeld:
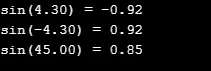
In de volgende broncode heb ik twee verschillende invoerwaarden gebruikt om de sinwaarde te berekenen en dubbel te retourneren.
#include
#include
int main()
(
double a;
double z;
a = 4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = -4.3;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
a = 45;
z = sin(a);
printf("sin(%.2lf) = %.2lf\n", a, z);
return 0;
)
Output:
2. sinh ()
Deze wiskundige functie berekent de trigonometrische tangensinuswaarde voor het gegeven getal.
Syntaxis:
double sinh(x);
Voorbeeld
In de onderstaande broncode wordt Sinushyperbolisch berekend door een invoerwaarde aan te geven.
#include
#include
#define PI 3.141592654
int main()
(
double gt = 3.60, z;
z = sinh(gt);
printf("Sine hyperbolic of %.2lf is = %.2lf", gt, z);
return 0;
)
uitgang

3. cos ()
Deze wiskundige functie bepaalt de trigonometrische cosinuswaarde voor het gegeven element.
Syntaxis: return type cos(argument);
#include
#include
#define PI 3.14
int main()
(
double cVal, rVal, dVal;
for(int i=0;i<=2;i++)
(
printf(" Enter an Angle in degrees : ");
scanf("%lf", &dVal);
rVal = dVal * (PI/180);
cVal = cos(rVal);
printf("\n The Cosine value of %f = %f ", dVal, cVal);
printf("\n");
)
return 0;
)
Output:
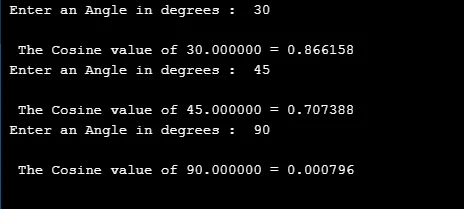
4. cosh ()
Het retourneert hyberbolische cosinus voor een bepaalde waarde.
Syntaxis:
double cosh(y);
Voorbeeld
Het onderstaande voorbeeld laat zien dat er twee verschillende invoerwaarden nodig zijn om hyperbolisch te berekenen.
#include
#include
int main ()
(
double k, r;
k = 0.6;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
k = -0.8;
r = cosh(k);
printf("Hyperbolic cosine of %lf is = %lf\n", k, r);
return 0;)
uitgang

5. kleurtje ()
Deze wiskundige bibliotheekfunctie berekent raaklijnwaarden van de hoek voor de wiskundige uitdrukking en gemeten in radialen.
Het kan worden verklaard als
double tan(arguments);
Voorbeeld
In de volgende broncode wordt de tan-waarde berekend voor de volgende hoeken, die wordt verhoogd met behulp van voor lus.
# include
# include
# include
void main()
(
float z ;
int k ;
char ch ;
printf("\nAngle \t Tan \n") ;
for (k = 0; k <= 180; k = k + 30)
(
z = k * 3.14159 / 180 ;
printf("\n %d, %5.2f", k, tan(z));
)
getch() ;
)
Output:
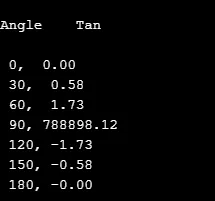
6. tanh ()
tanh () functie retourneert hyperbolische tangens van de gegeven waarde. Het duurt een enkele parameter. Naast het vinden van tangens voor lange dubbele en float worden tanhl () en tanhf () gebruikt voor de berekening.
Syntaxis:
double tanh( val);
Voorbeeld:
Een raaklijnhyberbolisch wordt berekend voor 'j'-waarden met behulp van voor lussen. Laten we kijken hoe het werkt.
#include
#include
#define PI 3.141592654
int main()
(
double val, r;
for(double j=0.60; j<=2.0;j+=.30)
(
r = tanh(j);
printf("Tangent hyperbolic of %.2lf is = %.2lf", j, r);
printf("\n");
)
return 0;
)
Output:
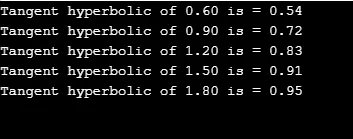
Log rekenkundige functies
Hieronder staan de verschillende functies van logaritmetiek:
1. exp ()
Deze functie berekent exponentieel voor een gegeven waarde (e x ). Er zijn ook andere subtypen zoals frexp (), Idexp () die mantisse retourneren en vermenigvuldigd met de macht van x.
Syntaxis:
return type exp(value);
Voorbeeld:
Het programma neemt een numerieke waarde van de gebruiker om de exponent voor een gegeven waarde te berekenen en geeft het dubbele terug.
#include
#include
int main()
(
double numb, eVal;
printf(" Enter any Numeric Value : ");
scanf("%lf", &numb);
eVal = exp(numb);
printf("\n Exponential Value of e power %lf = %lf ", numb, eVal);
printf("\n");
return 0;
)
uitgang

2. log ()
Deze functie retourneert de logaritmewaarde van een bepaald getal. (naar de basis e. log e )
Syntaxis:
double log(arg);
Voorbeeld:
In het volgende voorbeeld wordt de logboekwaarde voor het opgegeven nummer berekend met de functie. Door de gebruiker gedefinieerde functie lgm () berekent en functie wordt in de hoofdfunctie aangeroepen.
#include
#include
float lgm ( float iv );
int main ()
(
float q, r ;
printf ( "\nEnter a number to find log value \n");
scanf ( "%f", &q ) ;
r = lgm ( q ) ;
printf ( "\nthe log value is %f is %f", q, r );
)
float lgm ( float iv ) // function definition
(
float exe ;
exe = log(iv);
return ( exe ) ;
)
output:
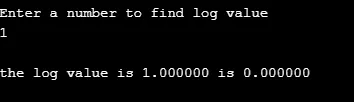
Conclusie
Tot slot hebben we verschillende wiskundige functies gezien die worden gebruikt in C-programmering en dit zijn de directe bibliotheekfuncties die moeten worden gebruikt. C-programma's gebruiken deze functies voor verschillende wiskundige bewerkingen. Om sommige complexe versies van berekeningen op te lossen, profiteert deze ingebouwde functie van de wiskundig georiënteerde programmeertaal om eenvoudige waarden te retourneren.
Aanbevolen artikelen
Dit is een gids voor wiskundige functies in C. Hier bespreken we verschillende wiskundige functies in C met voorbeelden. U kunt ook onze andere voorgestelde artikelen doornemen -
- PHP wiskundige functies
- JavaScript-wiskundige functies
- Overdrachtsfuncties in Matlab
- JavaScript-stringfuncties
- Inleiding tot wiskundige functies in Python
- Overzicht van wiskundige functies in C #
- C Matrixvermenigvuldiging programmeren
- Vierkantswortel in PHP
- Voorbeelden van vierkantswortel in JavaScript