
Inleiding tot binomiale distributie in R
Dit artikel beschrijft hoe binomiale distributies in R kunnen worden gebruikt voor de enkele bewerkingen die te maken hebben met waarschijnlijkheidsverdelingen. Business Analysis maakt gebruik van binomiale waarschijnlijkheid voor een complex probleem. R heeft tal van ingebouwde functies voor het berekenen van binomiale verdelingen die worden gebruikt bij statistische interferentie. De binomiale verdeling ook bekend als Bernoulli-proeven vereist twee soorten succes p en mislukking S. Het belangrijkste doel van het binomiale distributiemodel is dat ze de mogelijke waarschijnlijkheidsresultaten berekenen door een specifiek aantal positieve mogelijkheden te monitoren door het proces een bepaald aantal keren te herhalen . Ze moeten twee mogelijke resultaten hebben (succes / falen), daarom is de uitkomst dichotoom. De vooraf gedefinieerde wiskundige notatie is p = succes, q = 1-p.
Er zijn vier functies gekoppeld aan Binomiale distributies. Ze zijn dbinom, pbinom, qbinom, rbinom. De opgemaakte syntaxis wordt hieronder gegeven:
Syntaxis
- dbinom (x, maat, prob)
- pbinom (x, maat, prob)
- qbinom (x, size, prob) of qbinom (x, size, prob, lower_tail, log_p)
- rbinom (x, maat, prob)
De functie heeft drie argumenten: de waarde x is een vector van kwantielen (van 0 tot n), grootte is het aantal pogingen van paden, prob geeft waarschijnlijkheid voor elke poging aan. Laten we een voor een kijken met een voorbeeld.
1) dbinom ()
Het is een dichtheids- of distributiefunctie. De vectorwaarden moeten een geheel getal zijn en mogen geen negatief getal zijn. Deze functie probeert een aantal successen te vinden in een nee. van proeven die zijn vastgesteld.
Een binomiale verdeling heeft de grootte- en x-waarden. bijvoorbeeld, grootte = 6, de mogelijke x-waarden zijn 0, 1, 2, 3, 4, 5, 6, hetgeen P (X = x) impliceert.
n <- 6; p<- 0.6; x <- 0:n
dbinom(x, n, p)
Output:
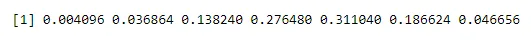
Een kans maken op één
n <- 6; p<- 0.6; x <- 0:n
sum(dbinom(x, n, p))
Output:
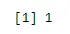
Voorbeeld 1 - Uit de ziekenhuisdatabase blijkt dat 65% van de patiënten met kanker sterft. Hoe groot is de kans dat van 5 willekeurig gekozen patiënten waarvan 3 herstellen?
Hier passen we de dbinom-functie toe. De kans dat 3 zal herstellen met behulp van dichtheidsverdeling op alle punten.
n = 5, p = 0, 65, x = 3
dbinom(3, size=5, prob=0.65)
Output:

Voor x waarde 0 tot 3:
dbinom(0, size=5, prob=0.65) +
+ dbinom(1, size=5, prob=0.65) +
+ dbinom(2, size=5, prob=0.65) +
+ dbinom(3, size=5, prob=0.65)
Output:
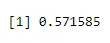
Maak vervolgens een steekproef van 40 papieren en incrementeel met 2 en maak ook binomiaal met dbinom.
a <- seq(0, 40, by = 2)
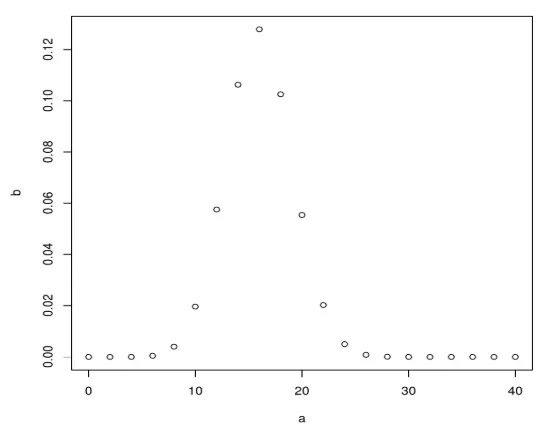
b <- dbinom(a, 40, 0.4)
plot(a, b)
Het produceert de volgende uitvoer na het uitvoeren van de bovenstaande code. De binomiale verdeling wordt uitgezet met behulp van de plot () functie.
Voorbeeld 2 - Beschouw een scenario, laten we aannemen dat de kans dat een student een boek uit een bibliotheek uitleent 0, 7 is. Er zijn 6 studenten in de bibliotheek, wat is de kans dat 3 van hen een boek lenen?
hier P (X = 3)
Code:
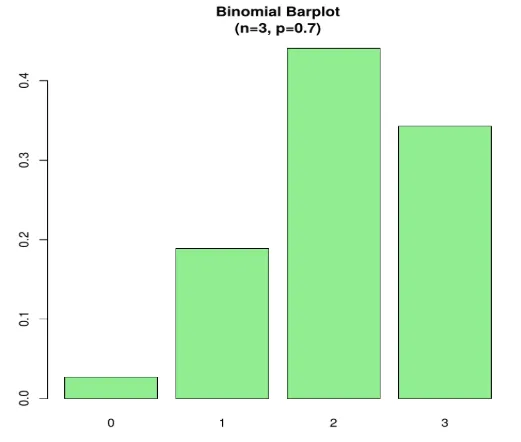
n=3; p=.7; x=0:n; prob=dbinom(x, n, p);
barplot(prob, names.arg = x, main="Binomial Barplot\n(n=3, p=0.7)", col="lightgreen")
Onder Plot wordt weergegeven wanneer p> 0, 5, daarom is binomiale verdeling positief scheef zoals weergegeven.
Output:
2) Pbinom ()
berekent cumulatieve kansen van binomiaal of CDF (P (X <= x)).
Voorbeeld 1:
x <- c(0, 2, 5, 7, 8, 12, 13)
pbinom(x, size=20, prob=.2)
Output:

Voorbeeld 2: Dravid scoort een wicket op 20% van zijn pogingen wanneer hij bowt. Als hij 5 keer bowt, hoe groot is dan de kans dat hij 4 of minder wicket scoort?
De kans op succes is hier 0, 2 en gedurende 5 pogingen die we krijgen
pbinom(4, size=5, prob=.2)
Output:
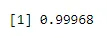
Voorbeeld 3: 4% van de Amerikanen is zwart. Zoek de kans op 2 zwarte studenten bij het willekeurig selecteren van 6 studenten uit een klas van 100 zonder vervanging.
Wanneer R: x = 4 R: n = 6 R: p = 0. 0 4
pbinom(4, 6, 0.04)
Output: -
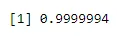
3) qbinom ()
Het is een kwantiele functie en doet het omgekeerde van de cumulatieve waarschijnlijkheidsfunctie. De cumulatieve waarde komt overeen met een waarschijnlijkheidswaarde.
Voorbeeld: Hoeveel staarten hebben een kans van 0, 2 wanneer een munt 61 keer wordt gegooid.
a <- qbinom(0.2, 61, 1/2)
print(a)
Output: -
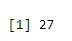
4) rbinom ()
Het genereert willekeurige getallen. Verschillende uitkomsten produceren verschillende willekeurige uitvoer, gebruikt in het simulatieproces.
Voorbeeld:-
rbinom(30, 5, 0.5)
rbinom(30, 5, 0.5)
Output: -

Elke keer dat we het uitvoeren, geeft het willekeurige resultaten.
rbinom(200, 4, 0.4)
Output: -

Hier doen we dit door in een enkele poging de uitkomst van 30 muntjes om te slaan.
rbinom(30, 1, 0.5)
Output: -
Barplot gebruiken:
a<-rbinom(30, 1, 0.5)
print(a)
barplot(table(a),>
Output: -
Om het gemiddelde van succes te vinden
output <-rbinom(10, size=60, 0.3)
mean(output)
Output: -
Conclusie - Binomiale verdeling in R
Daarom hebben we in dit document de binomiale verdeling in R besproken. We hebben gesimuleerd met behulp van verschillende voorbeelden in R studio- en R-fragmenten en ook de ingebouwde functies beschreven die helpen bij het genereren van binomiale berekeningen. Binomiale verdeling berekening in R maakt gebruik van statistische berekeningen. Daarom helpt een binomiale verdeling bij het vinden van waarschijnlijkheid en willekeurig zoeken met behulp van een binomiale variabele.
Aanbevolen artikelen
Dit is een gids voor Binomiale distributie in R. Hier hebben we een inleiding besproken en de functies ervan in verband met Binomiale distributie samen met de syntaxis en geschikte voorbeelden. U kunt ook onze andere voorgestelde artikelen doornemen voor meer informatie -
- Binomiale distributieformule
- Economie versus bedrijf
- Bedrijfsanalysetechnieken
- Linux-distributies