Lineaire regressie in Excel - Hoe lineaire regressie te doen in Excel?

Lineaire regressie in Excel (inhoudsopgave)

Inleiding tot lineaire regressie in Excel
Methoden voor het gebruik van lineaire regressie in Excel

Inleiding tot lineaire regressie in Excel

Lineaire regressie is een statistische techniek / methode die wordt gebruikt om de relatie tussen twee continue kwantitatieve variabelen te bestuderen. In deze techniek worden onafhankelijke variabelen gebruikt om de waarde van een afhankelijke variabele te voorspellen. Als er slechts één onafhankelijke variabele is, is het een eenvoudige lineaire regressie, en als een aantal onafhankelijke variabelen meer dan één zijn, is het een meervoudige lineaire regressie. Lineaire regressiemodellen hebben een relatie tussen afhankelijke en onafhankelijke variabelen door een lineaire vergelijking aan te passen aan de waargenomen gegevens. Lineair verwijst naar het feit dat we een lijn gebruiken om onze gegevens te passen. De afhankelijke variabelen die worden gebruikt in regressieanalyse worden ook respons- of voorspelde variabelen genoemd en onafhankelijke variabelen worden ook verklarende variabelen of voorspellers genoemd.

Een lineaire regressielijn heeft een vergelijking van het type: Y = a + bX;

Waar:

X is de verklarende variabele,
Y is de afhankelijke variabele,
b is de helling van de lijn,
a is y-onderscheppen (dat wil zeggen de waarde van y wanneer x = 0).

De methode met de kleinste kwadraten wordt meestal gebruikt in lineaire regressie die de best passende lijn voor waargenomen gegevens berekent door de som van de afwijkingsvierkanten van gegevenspunten te minimaliseren.

Methoden voor het gebruik van lineaire regressie in Excel

Dit voorbeeld leert u de methoden voor het uitvoeren van lineaire regressieanalyse in Excel. Laten we een paar methoden bekijken.

U kunt deze Excel-sjabloon voor lineaire regressie hier downloaden - Excel-sjabloon voor lineaire regressie

Methode # 1 - spreidingsdiagram met een trendlijn

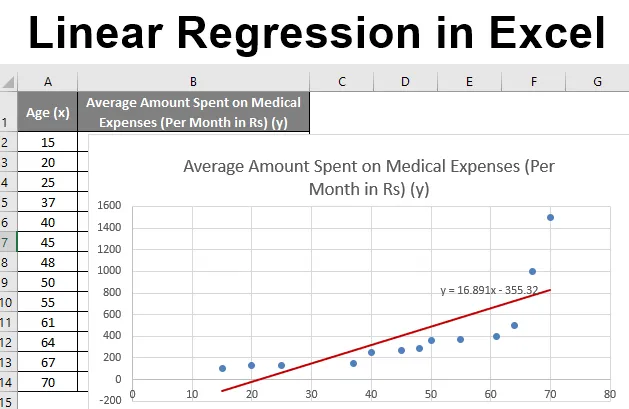
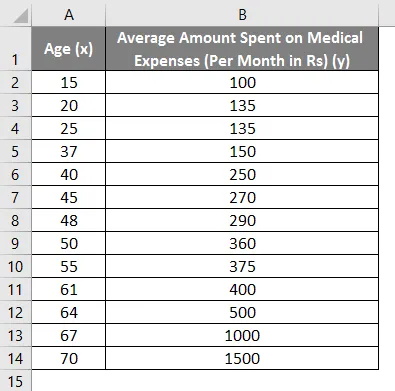
Laten we zeggen dat we een dataset hebben van sommige personen met hun leeftijd, bio-massa-index (BMI) en het bedrag dat ze in een maand aan medische uitgaven hebben uitgegeven. Nu met een inzicht in de kenmerken van de individuen zoals leeftijd en BMI, willen we ontdekken hoe deze variabelen de medische kosten beïnvloeden, en deze daarom gebruiken om regressie uit te voeren en de gemiddelde medische kosten voor sommige specifieke individuen te schatten / voorspellen. Laten we eerst kijken hoe alleen leeftijd de medische kosten beïnvloedt. Laten we de dataset bekijken:

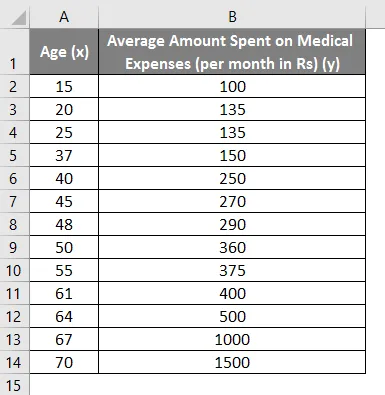
Bedrag aan medische kosten = b * leeftijd + a

Selecteer de twee kolommen van de gegevensset (x en y), inclusief headers.

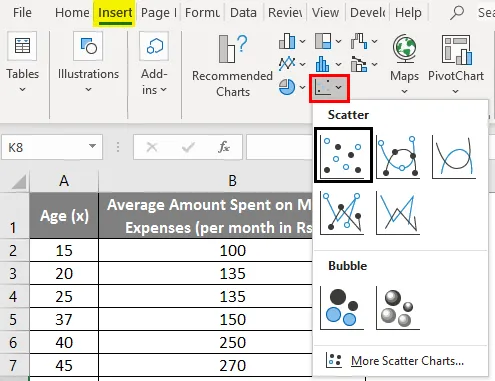
Klik op 'Invoegen' en vouw de vervolgkeuzelijst voor 'Scatter Chart' uit en selecteer 'Scatter' thumbnail (eerste)

Nu zal een spreidingsdiagram verschijnen en we zouden de regressielijn hierop trekken. Klik hiertoe met de rechtermuisknop op een willekeurig gegevenspunt en selecteer 'Trendlijn toevoegen'

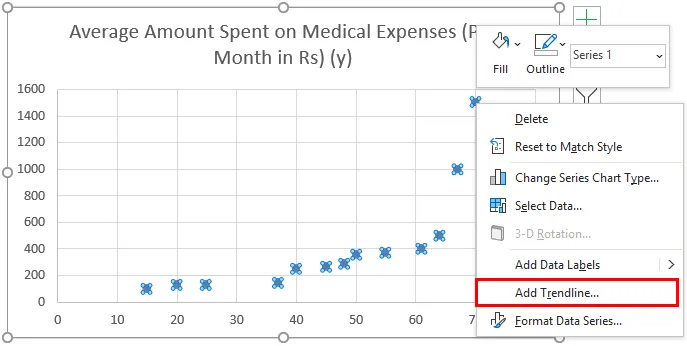
Selecteer nu in het deelvenster 'Trendlijn opmaken', 'Lineaire trendlijn' en 'Vergelijking weergeven op grafiek'.

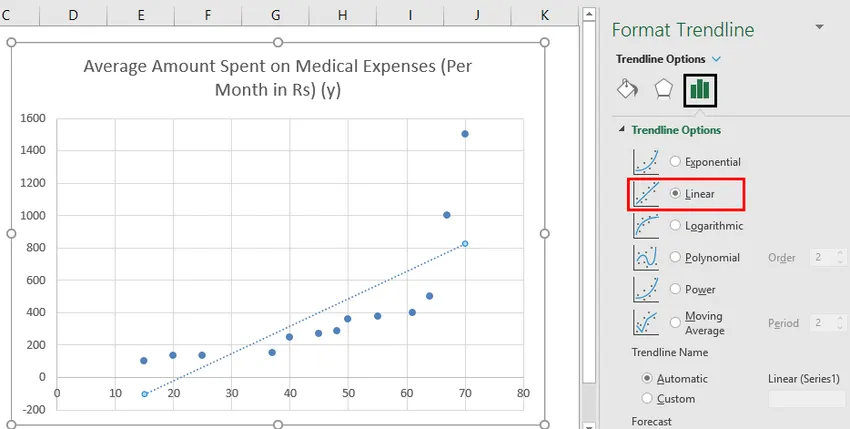
Selecteer 'Vergelijking weergeven op kaart'.

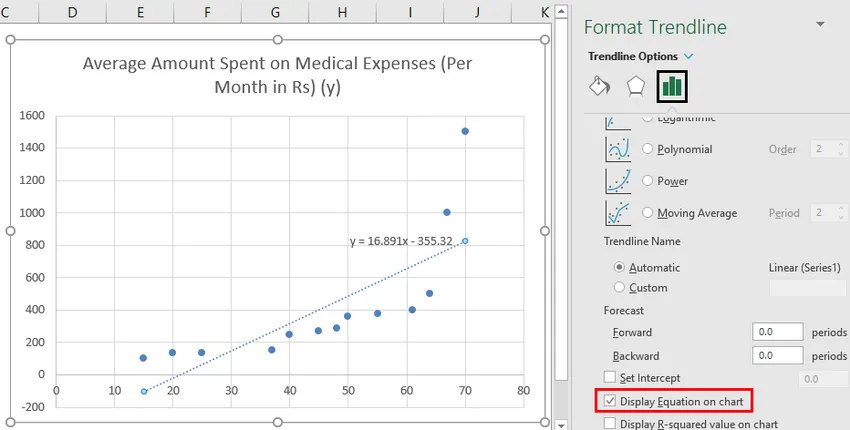
We kunnen de grafiek improviseren volgens onze vereisten, zoals het toevoegen van bijentitels, het wijzigen van de schaal, kleur en lijntype.

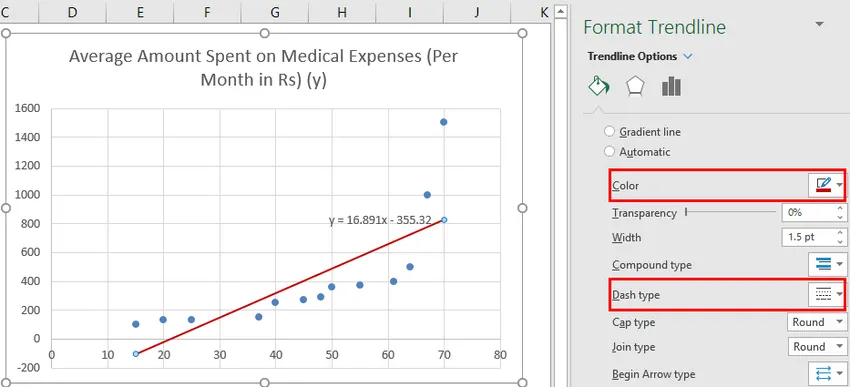
Na het improviseren van de grafiek is dit de output die we krijgen.

Opmerking: In dit type regressiegrafiek moet de afhankelijke variabele zich altijd op de y-as bevinden en onafhankelijk van de x-as. Als de grafiek in omgekeerde volgorde wordt uitgezet, wissel dan de assen in een grafiek of verwissel de kolommen in de gegevensset.

Methode # 2 - Analyse ToolPak Add-In Methode

Analysis ToolPak is soms niet standaard ingeschakeld en we moeten dit handmatig doen. Om dit te doen:

Klik op het menu 'Bestand'.

Klik daarna op 'Opties'.

Selecteer 'Excel-invoegtoepassingen' in het vak 'Beheren' en klik op 'Ga'

Selecteer 'Analysis ToolPak' -> 'OK'

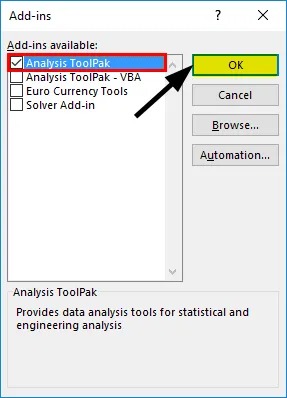
Hiermee voegt u 'Data Analysis'-tools toe aan het tabblad' Data '. Nu voeren we de regressieanalyse uit:

Klik op 'Gegevensanalyse' op het tabblad 'Gegevens'

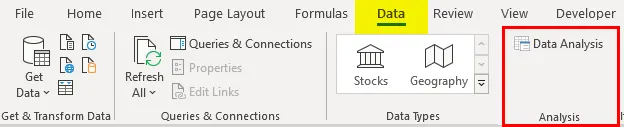
Selecteer 'Regression' -> 'OK'

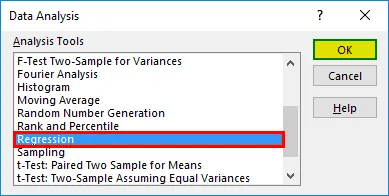
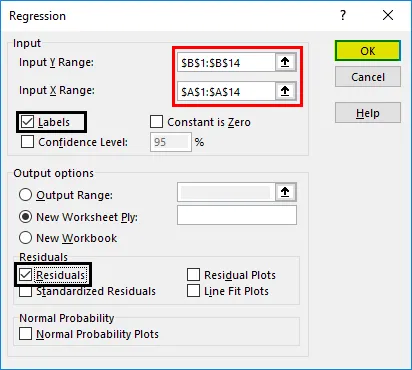
Er verschijnt een regressiedialoogvenster. Selecteer het Input Y-bereik en Input X-bereik (respectievelijk medische kosten en leeftijd). In het geval van meervoudige lineaire regressie, kunnen we meer kolommen met onafhankelijke variabelen selecteren (bijvoorbeeld als we de impact van BMI op de medische kosten willen zien).
Vink het vakje 'Labels' aan om headers toe te voegen.
Kies de gewenste 'output'-optie.
Schakel het selectievakje 'residuen' in en klik op 'OK'.

Nu wordt onze output van de regressieanalyse gemaakt in een nieuw werkblad met de regressiestatistieken, ANOVA, residuen en de coëfficiënten.

Uitgangsinterpretatie:

Regressiestatistieken vertellen hoe goed de regressievergelijking past bij de gegevens:

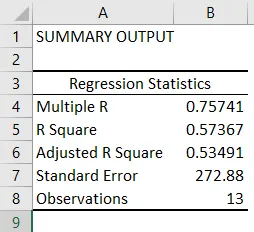
Meervoudige R is de correlatiecoëfficiënt die de sterkte van de lineaire relatie tussen twee variabelen meet. Het ligt tussen -1 en 1, en de absolute waarde geeft de relatiesterkte weer met een grote waarde die een sterkere relatie aangeeft, een lage waarde die negatief aangeeft en een nulwaarde die geen relatie aangeeft.
R-vierkant is de bepalingscoëfficiënt die wordt gebruikt als een indicator voor de goede pasvorm. Het ligt tussen 0 en 1, met een waarde dicht bij 1 die aangeeft dat het model goed past. In dit geval wordt 0, 57 = 57% van de y-waarden verklaard door de x-waarden.
Aangepast R-vierkant is R-vierkant aangepast voor het aantal voorspellers in geval van meervoudige lineaire regressie.
Standaardfout geeft de precisie van regressieanalyse weer.
Observations geeft het aantal modelobservaties weer.
Anova vertelt het niveau van variabiliteit binnen het regressiemodel.

Dit wordt over het algemeen niet gebruikt voor eenvoudige lineaire regressie. De 'Significance F-waarden' geven echter aan hoe betrouwbaar onze resultaten zijn, met een waarde groter dan 0, 05 die suggereert om een andere voorspeller te kiezen.

Coëfficiënten is het belangrijkste onderdeel dat wordt gebruikt om een regressievergelijking op te bouwen.

Dus onze regressievergelijking zou zijn: y = 16.891 x - 355.32. Dit is hetzelfde als dat gedaan door methode 1 (spreidingsdiagram met een trendlijn).

Als we nu de gemiddelde medische kosten willen voorspellen wanneer de leeftijd 72 is:

Dus y = 16.891 * 72 -355.32 = 860.832

Op deze manier kunnen we waarden van y voorspellen voor alle andere waarden van x.

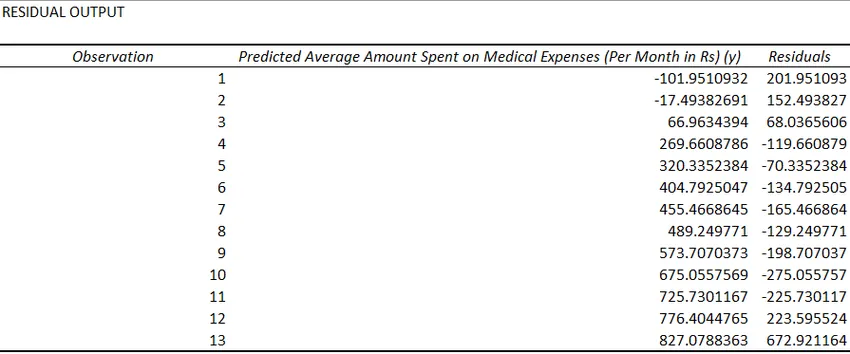
Residuen geven het verschil aan tussen werkelijke en voorspelde waarden.

De laatste methode voor regressie wordt niet zo vaak gebruikt en vereist statistische functies zoals slope (), intercept (), correl (), enz. Om regressieanalyses uit te voeren.

Dingen om te onthouden over lineaire regressie in Excel

Regressieanalyse wordt over het algemeen gebruikt om te zien of er een statistisch significante relatie is tussen twee sets variabelen.
Het wordt gebruikt om de waarde van de afhankelijke variabele te voorspellen op basis van waarden van een of meer onafhankelijke variabelen.
Wanneer we een lineair regressiemodel aan een groep gegevens willen aanpassen, moet het gegevensbereik zorgvuldig worden geobserveerd alsof we een regressievergelijking gebruiken om een waarde buiten dit bereik te voorspellen (extrapolatie), dan kan dit tot verkeerde resultaten leiden.

Aanbevolen artikelen

Dit is een gids voor lineaire regressie in Excel. Hier bespreken we hoe u lineaire regressie in Excel kunt doen, samen met praktische voorbeelden en een downloadbare Excel-sjabloon. U kunt ook onze andere voorgestelde artikelen doornemen -