Samenvoegen Sorteren in JavaScript - Verschillende soorten eigenschappen

Inleiding tot samenvoegen Sorteren in JavaScript

Sorteeralgoritmen zijn erg belangrijk in de informatica. De uitvoer van sorteren is om de elementen van een lijst in een bepaalde volgorde (oplopend of aflopend) te rangschikken. Sorteer samenvoegen in JavaScript is een van de meest efficiënte sorteeralgoritmen die beschikbaar zijn, omdat het gebaseerd is op het concept van verdeel en overwint. Zoals de naam al doet vermoeden, verdeel je eerst het grotere probleem in kleine problemen dan het oplossen van de kleinere problemen om het grotere probleem op te lossen. Conceptueel is het samenvoegen een combinatie van twee basisalgoritmen genaamd MERGE en MERGE_SORT.

die werkt als volgt:

Verdeel de ongesorteerde lijst in n aantal sublijsten met één item (n is het totale aantal elementen in de ongesorteerde lijst).
Voeg sublijsten herhaaldelijk samen in gesorteerde sublijsten totdat er slechts één gesorteerde lijst is.

Implementatie van Merge Sort in JavaScript

Het MERGE-algoritme volgt de procedure van het combineren van twee gesorteerde lijsten in één gesorteerde lijst.

Voorbeeld: stel dat er twee lijsten zijn, dwz lijst 1 (1, 5, 3) en lijst 2 (7, 2, 9).

1. Sorteer eerst beide lijsten.

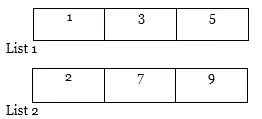
Nu zullen we de E-techniek erop zien en toepassen.

2. Vervolgens maken we een nieuwe lijst met grootte x + y waarbij x het aantal elementen in lijst 1 is en y het aantal elementen in lijst 2 is.

In ons geval x = 3 en y = 3, dus x + y = 6.

3. Nu hebben we twee aanwijzingen.
Een eerste aanwijzer die naar de eerste positie van lijst 1 wijst en een tweede aanwijzer die naar de eerste positie van lijst 2 wijst.

4. Vervolgens vergelijken we de waarde van beide pointers. De aanwijzer met lagere waarde, kopieer dat element naar lijst 3 en verplaats de aanwijzer naar rechts van de lijst met kleinere waarde en de resulterende lijst (dwz lijst 1 en lijst 3)

5. Voer op dezelfde manier stap 4 steeds opnieuw uit.

Verder reizen …

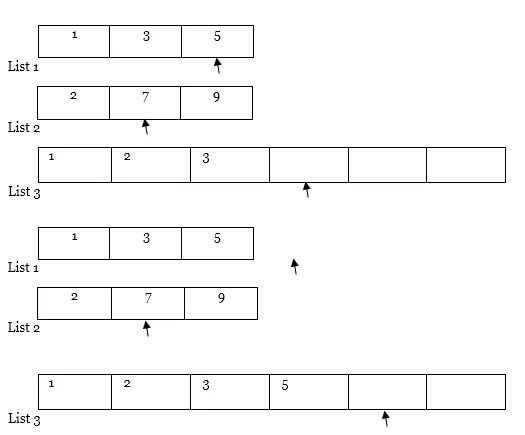
Opmerking : als een van de lijsten (dwz lijst 1 of lijst 2) volledig wordt doorlopen zoals in het geval, kopieer dan de volledige inhoud van een andere lijst van de aanwijzer naar de resultatenlijst (dwz lijst 3) als volgt.

pseudocode

Function merge (sublist1, sublist2) ( Create var for result list While sublist1 length > 0 and sublist2 length > 0 If sublist1(0) < sublist2(0) Copy the sublist1 pointer value to result list and Shift pointer of sublist1 to right else Copy the sublist2 pointer value to result list and Shift pointer of sublist2 to right Return concat sublist1 or sublist2 (depending if node1 is empty or not)

Het MERGE_SORT-algoritme verdeelt de gegeven ongesorteerde lijst naar minimale grootte en roept vervolgens het MERGE-algoritme op om de lijst te combineren in de nieuwe gesorteerde lijst.

pseudocode

function mergeSort(list) ( If list length < 2 Return list Create var for middle index of list Create var for left index of list Create var for right index of list Recursively call mergeSort function )

Voorbeeld

Hier volgen we de top-down Merge Sort-implementatie. Het begint bovenaan en gaat verder naar beneden, waarbij elke recursieve beurt dezelfde vraag stelt: "Wat moet er gedaan worden om de lijst te sorteren?" resultaten”.

Code in Javascript

// Split the list into halves and merge them recursively function mergeSort (list) ( if (list.length < 2) ( return list;// return once we hit a list with a single element ) var mid = Math.floor(list.length / 2); var left = mergeSort(list.slice(0, mid)); var right = mergeSort(list.slice(mid)); return merge(left, right); ) // compare the lists element by element and return the concatenated resultList function merge (sublist1, sublist2) ( var resultList = (); while (sublist1.length > 0 && sublist2.length > 0) resultList.push(sublist1(0) < sublist2(0)? sublist1.shift() : sublist2.shift()); return resultList.concat(sublist1.length? sublist1 : sublist2); ) const list = (6, 5, 3, 1, 8, 7, 2, 4, 2, 5, 1, 2, 3) console.log(mergeSort(list)) //( 1, 1, 2, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8 )

De hoofdfunctie van de merge-sortering verdeelt de gegeven lijst in kleinere lijsten bij elke iteratie van de recursieve aanroep. Vergeet niet dat recursie de basisvoorwaarde vereist om oneindige recursie te voorkomen. In ons geval hebben we:

if (list.length < 2) ( return list;// return once we hit a list with a single element )

Nadat we de basisvoorwaarde voor recursie hebben ingesteld, zullen we de middelste index identificeren om de gegeven lijst in de linker en rechter sublijst te splitsen, zoals u hierboven in het voorbeelddiagram kunt zien. Dan moeten we de linker sublijst samenvoegen en de rechter sublijst die we nu zullen bekijken. In de bovenstaande samenvoegfunctie moeten we ervoor zorgen dat we alle elementen in de linker sublijst en de rechter sublijst sorteren lijst. De manier waarop we dit doen, is door een while-lus te gebruiken. Binnen de while-lus vergelijken we het element in de linker sublijst en het element in de rechter sublijst één voor één. We kunnen de kleinste van de twee in de resultatenlijst duwen en de cursor van de linker sublijst en de rechter sublijst dienovereenkomstig verplaatsen. Ten slotte moeten we de resultatenlijst samenvoegen. Dit is erg belangrijk! Als we deze laatste stap hier niet doen, hebben we aan het eind een onvolledige lijst van elementen omdat de voorwaarde while lus zal mislukken wanneer een van de twee aanwijzers het einde bereikt.

Output:

Eigenschappen van Merge Sort

Het samenvoegen is stabiel omdat hetzelfde element in een array hun oorspronkelijke posities ten opzichte van elkaar behoudt.
Sorteren samenvoegen is niet 'op zijn plaats' omdat tijdens het samenvoegen er een kopie van de hele lijst wordt gesorteerd. Hierdoor is de ruimtecomplexiteit (O (n)) van dit algoritme eigenlijk groter dan die van andere, en niet te gebruiken in complexe problemen waar ruimte premium is.
De algehele tijdcomplexiteit van Merge-sortering is O (nLogn). Het is efficiënter omdat het in het slechtste geval ook is, de looptijd is O (nlogn).

Conclusie

Samenvoegen sorteer beste, slechtste en gemiddelde case tijd complexiteiten zijn hetzelfde, waardoor het een efficiënter algoritme is. Het werkt sneller dan andere sorteertechnieken. Het samenvoegen kan worden toegepast op bestanden van elke grootte. Het is in hoge mate parallelliseerbaar door het gebruik van de verdeel-en-verover-methode. Om sterke basisprincipes in de informatica te ontwikkelen, wordt u geadviseerd om verschillende sorteeralgoritmen grondig te begrijpen.

Aanbevolen artikel

Dit is een gids voor Sorteer samenvoegen in JavaScript. Hier bespreken we de introductie van samenvoegen sorteren in JavaScript en de implementatie samen met eigenschappen. U kunt ook onze andere voorgestelde artikelen doornemen voor meer informatie -