
Inleiding tot overdrachtsfuncties in Matlab
Een overdrachtsfunctie wordt voorgesteld door 'H (s)'. H (s) is een complexe functie en 's' is een complexe variabele. Het wordt verkregen door de Laplace-transformatie van impulsresponsie h (t) te nemen. overdrachtsfunctie en impulsrespons worden alleen gebruikt in LTI-systemen. LTI-systeem betekent lineair en tijdinvariant systeem, volgens de lineaire eigenschap, aangezien de invoer nul is, wordt de uitvoer ook nul. Als we dus niet denken dat de beginvoorwaarden nul zijn, mislukt de lineaire eigenschap en als de eigenschap faalt, wordt het systeem niet-lineair. Vanwege het niet-lineariteitssysteem wordt het niet-LTI-systeem. En voor niet-LTI-systemen kunnen we de overdrachtsfunctie niet definiëren, daarom is het verplicht om aan te nemen dat de initiële voorwaarden nul zijn.
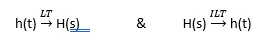
Definitie van overdrachtsfuncties in Matlab
De overdrachtsfunctie van het LTI-systeem is de verhouding van Laplace-transformatie van uitvoer tot de Laplace-transformatie van invoer van het systeem door aan te nemen dat alle beginvoorwaarden nul zijn.

In het bovenstaande systeem is de invoer x (t) en is de uitvoer y (t). Na het nemen van Laplace Transform van het hele systeem, wordt x (t) X (s), y (t) wordt Y (s). We beschouwen alle beginvoorwaarden als nul omdat

Methoden van overdrachtsfuncties in Matlab
Er zijn drie methoden om de overdrachtsfunctie in Matlab te verkrijgen
- Door vergelijking te gebruiken
- Door coëfficiënten te gebruiken
- Door Pole Zero gain te gebruiken
Laten we een voorbeeld bekijken
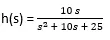
1) Door vergelijking te gebruiken
Eerst moeten we verklaren dat 's' een overdrachtsfunctie is en typ vervolgens de hele vergelijking in het opdrachtvenster of de Matlab-editor. In deze 's' staat de overdrachtsfunctievariabele.
Commando: "tf"
Syntaxis : transfer function variable name = tf('transfer function variable name');
Voorbeeld: s = tf ('s');
Matlab-programma
2) Door coëfficiënten te gebruiken
In deze methode worden teller en noemer coëfficiënten gebruikt, gevolgd door het commando 'tf'.
In het bovenstaande voorbeeld
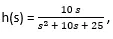
De teller heeft slechts één waarde die "10s" is, dus de coëfficiënt is 10.
En in de noemer zijn er drie termen “, dus coëfficiënten zijn 1, 10 en 25.
Commando: "tf"
Syntaxis : transfer function variable name = tf((numerator coefficients ), (denominator coefficients))
Voorbeeld: h = tf ((10 0), (1 10 25);
3) Door Pole Zero gain te gebruiken
In deze methode gebruiken we het commando “zpk”, hier staat z voor nullen, p staat voor polen en k staat voor versterking.
In bovenstaand voorbeeld:
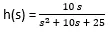
Zeros:
N = 0
10 * s = 0
(S- 0) = 0
Hier is winst 10 en
s = 0
daarom nul aanwezig bij oorsprong
D = 0
S 2 + 10s + 25 = 0
S + 5s + 5s + 25 = 0
S (s + 5) + 5 (s + 5) = 0
(s + 5) (s + 5) = 0
S = -5, -5
Daarom zijn er twee polen aanwezig op -5.
commando: zpk
syntaxis: zpk ((nullen), (polen), gain)
voorbeeld: zpk ((0), (- 5 -5), 10)
Voorbeelden & syntaxis van overdrachtsfuncties in Matlab
Hieronder staan de verschillende voorbeelden van overdrachtsfuncties met hun syntaxis:
Voorbeeld 1
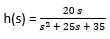
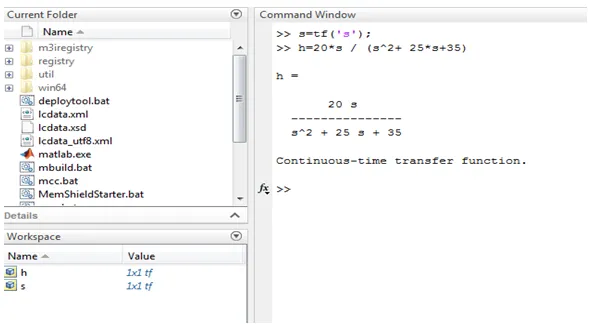
Het bovenstaande voorbeeld geïllustreerd in scherm 1. in deze overdrachtsfunctie weergegeven door vergelijking en het commando 'tf' wordt gebruikt. Waarden van h en s worden opgeslagen in de werkruimte.
Voorbeeld 2
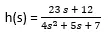
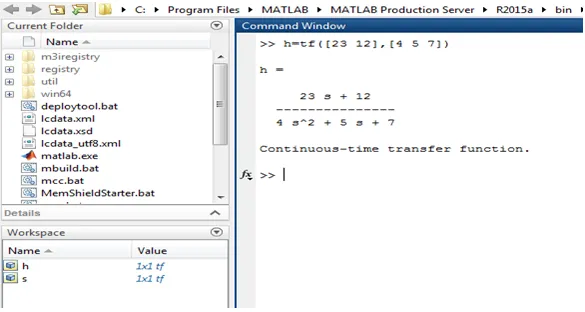
In dit voorbeeld wordt de coëfficiëntmethode gebruikt. Daarom moeten we eerst de teller en noemer afzonderlijk vinden. Hier is de teller 23s + 12 en de coëfficiënt van de teller is 23 en 12. De noemer is en de coëfficiënten van de noemer zijn 4, 5 en 7
Onderstaande afbeelding toont het Matlab-programma voor het bovenstaande voorbeeld.
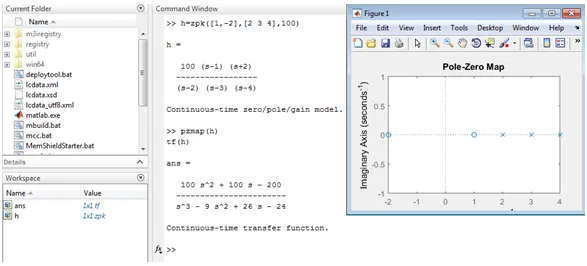
Voorbeeld 3
In dit voorbeeld zijn invoer waarden van pool, nul en versterking, wordt het zpk-commando gebruikt om de overdrachtsfunctie te achterhalen.
Nullen = 1, -2
Palen = 2, 3, 4
Versterking = 100
Het toont output
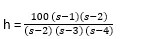
voordelen
- Het is een wiskundig model dat Gain of LTI-systeem geeft. wiskundige modellering en wiskundige vergelijkingen zijn nuttig om de prestaties, kenmerken en stabiliteit van het systeem te begrijpen
- Complexe integraalvergelijkingen en differentiaalvergelijkingen omgezet in de eenvoudige algebraïsche vergelijkingen (polynoomvergelijkingen)
- De overdrachtsfunctie is afhankelijk van het systeem en onafhankelijk van invoer.
- Als de overdrachtsfunctie van het systeem bekend is, kan de uitvoer eenvoudig worden berekend.
- Het geeft informatie over polen en nullen, kan worden berekend.
Conclusie
In dit artikel hebben we verschillende methoden bestudeerd om de overdrachtsfunctie in Matlab weer te geven die vergelijking, coëfficiënten en pool-nul versterkingsinformatie gebruiken. In de weergave Transfer Function kunnen we ook polen plotten, nul plotten met behulp van de opdracht 'pzmap'.
Deze weergave kan worden verkregen op beide manieren van vergelijkingen tot pool-nul plot en van pool-nul plot naar de vergelijking. Overdrachtsfunctie meestal gebruikt in besturingssystemen en signalen en systemen.
Aanbevolen artikelen
Dit is een gids voor overdrachtsfuncties in Matlab. Hier bespreken we de definitie, methoden van een overdrachtsfunctie, waaronder het gebruik van vergelijking, het gebruik van coëfficiënt en het gebruik van pool-nul versterking, samen met enkele voorbeelden. U kunt ook de volgende artikelen bekijken voor meer informatie -
- Terwijl Loop in Matlab
- Gegevenstypen in MATLAB
- Switch-verklaring in Matlab
- Matlab-operators
- Inline-functies in Matlab (syntaxis, voorbeelden)
- Matlab-compiler | Toepassingen van Matlab Compiler