Vectoren in Matlab - Soorten vectorbewerking met voorbeelden

Inleiding tot vectoren in Matlab

Een vector is een ingesloten set elementen. In Matlab kunnen we vectoren maken met vierkante haakjes. Vectoren zijn een van de illustraties van arrays (eendimensionale array). het kan op twee manieren worden weergegeven rijvector en kolomvector.

Rij Vector

Het is een horizontaal geheel van elementen. Het wordt weergegeven tussen vierkante haken. Elk element wordt gescheiden door een komma of spatie.

X = (4 7 8) of X = (4, 7, 8)

Kolom Vector

Het is een verticale set elementen. Het wordt ook weergegeven tussen vierkante haken. Er zijn twee manieren om eerst kolomvectoren te maken door elk element te scheiden door een puntkomma en een andere manier is om elk element op de volgende rij in het opdrachtvenster te schrijven.

X = (4; 6; 7) of

X = (4

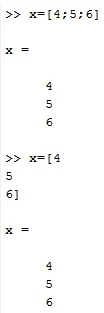
Vector operaties

Vectoroperators zijn grofweg in twee categorieën ingedeeld.

1. Rekenkundige bewerking

Laten we twee vectoren x en y beschouwen met waarden x = (1 4 5 3) en y = (5 3 2 1) we kunnen verschillende bewerkingen uitvoeren op deze twee vectoren x en y.

een. Vermenigvuldiging: deze functie wordt gebruikt om met elke rekenkundige waarde te vermenigvuldigen met de gehele vector.

Bijvoorbeeld:

mul = 3 * x

mul = 3 * (1 4 5 3)

mul = (3 12 15 9)

Syntaxis: variable name = arithmetic constant * vector name

b. Goniometrische functie: we kunnen elke goniometrische functie toepassen op vectorachtige sin, cos, tan, cosec, sec, enz.

Voorbeeld tri = cos (x)

Antwoord is: 0, 54 - 0, 65 0, 28 -0, 99

Syntaxis: variable name = trigonometric function name ( vector name )

Som: dit toont een totaal van (toevoeging van) hele elementen in één vector.

Voorbeeld

x = (1 4 5 3)

Totaal = som (x)

Uitgang is totaal = 13

Syntaxis: variable name = = sum ( vector name )

c. Lengte: het toont de lengte van een bepaalde vector, laten we een vector p = (9 7 5 3 1 9 7 5 3 1)

Voorbeeld

p = (9 7 5 3 1 9 7 5 3 1)

Len = lengte (p)

Uitgang is Len = 10

d. Toevoeging van vectoren: toevoeging van twee of meerdere vectoren is een eenvoudige bewerking in Matlab, laten we twee vectoren p en q beschouwen.

P = (4 6 3 2) en q = (5 7 9 1)

Toevoegen = p + q

Uitgang is Toevoegen = (9 13 12 3)

Syntaxis: vector name operator ( + ) vector name

Op dezelfde manier kunnen we aftrekken zoals sub = p - q

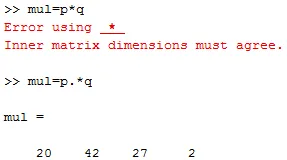
e. Vermenigvuldiging van vectoren: als we twee vectoren willen vermenigvuldigen, werkt een eenvoudige vermenigvuldigingsoperator (*) niet. Daarom moeten we een puntoperator ('.') Toevoegen met een vermenigvuldigingsoperator.

Voorbeeld:

P = (4 6 3 2) en q = (5 7 9 1)

mul = p. * q

uitgang is mul = (20 42 27 2)

Syntaxis: variable name = vector name dot operator multiplication operator vector name

Stel dat ik het kwadraat van een bepaalde vector wil weten of ik wil de vector alleen met die vector vermenigvuldigen.

De syntaxis is dan squr = x. 2

2. Relationele werking

een. Gelijk aan de operator : deze operator vergelijkt elk n elk element van twee vectoren en geeft output is nul en één vorm.

Voorbeeld

m = (2 5 8)

En n = (5 5 3)

Zoals we weten, zijn er drie elementen in vector m en vector n,

m == n

De bovenstaande instructie geeft output als 0 1 0, wat betekent dat eerste nee niet gelijk is, het tweede nummer gelijk is en het derde nee niet gelijk is. O staat voor onwaar en 1 staat voor waar.

b. Kleiner dan operator (<): Kleiner dan de operator vertegenwoordigt met het symbool '<'. we kunnen een gegeven matrix vergelijken met elke rekenkundige constante of met een andere vector.

Voorbeeld

m = (3 2 4)

n = (1 1 1)

m <n

de uitvoer is 0 0 0, wat betekent dat alle getallen groter zijn dan vector n.

en als m <10

dan is de uitvoer 1 1 1, wat betekent dat alle nummers kleiner zijn dan 10.

c. Groter dan operator (>): Groter dan de operator wordt weergegeven door het symbool ('>'). We kunnen een gegeven matrix vergelijken met elke rekenkundige constante of met een andere vector.

Voorbeeld:

M = (3 2 4)

N = (1 1 1)

m> n

De uitvoer is 1 1 1, wat betekent dat alle waarden groter zijn dan de waarden van vector n.

Conclusie - vectoren in Matlab

In Matlab kunnen we verschillende soorten vectoren maken waar we verschillende bewerkingen kunnen uitvoeren, zoals optellen, aftrekken, vermenigvuldigen, vierkant, vierkantswortel, macht, schalen, vectorvermenigvuldiging, puntproduct, enz.

Aanbevolen artikelen

Dit is een gids voor vectoren in Matlab. Hier bespreken we de soorten vectorbewerking, waaronder rekenkundige en relationele bewerking, samen met enkele voorbeelden. U kunt ook de volgende artikelen bekijken voor meer informatie -